- 1.
- Since f is an epimorphism from G to H, the fundamental
isomorphism theorem tells us that
G/kerf
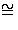 H, so in particular
| G/ker f| = | H|. Therefore
| G|/| ker f| = | H|,
hence
| ker f| = | G|/| H| and we deduce that
| kerf| = 33
H, so in particular
| G/ker f| = | H|. Therefore
| G|/| ker f| = | H|,
hence
| ker f| = | G|/| H| and we deduce that
| kerf| = 33  112. Using the fundamental theorem for
finitely generated abelian groups, we see that there are up to
isomorphism six abelian groups of order
| kerf| = 33
112. Using the fundamental theorem for
finitely generated abelian groups, we see that there are up to
isomorphism six abelian groups of order
| kerf| = 33  112, namely
112, namely
 /27 /27 X X
 /121 /121 |
 /9 /9 X X
 /3 /3 X X
 /121 /121 |
( /3 /3 )3 X )3 X
 /121 /121 |
 /27 /27 X
( X
( /11 /11 )2 )2 |
 /9 /9 X X
 /3 /3 X
( X
( /11 /11 )2 )2 |
( /3 /3 )3 X
( )3 X
( /11 /11 )2 )2 |
- 2.
- (i) Since A
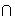 B is a subgroup of G whose order divides | A| = p4 and | B| = q5, we see that
| A
B is a subgroup of G whose order divides | A| = p4 and | B| = q5, we see that
| A 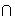 B| = 1 and hence
A
B| = 1 and hence
A 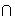 B = 1. Next if a
B = 1. Next if a  A and b
A and b  B, then
a-1b-1ab = (a-1b-1a)b
B, then
a-1b-1ab = (a-1b-1a)b  B, because B
B, because B 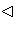 G.
Similarly
a-1b-1ab
G.
Similarly
a-1b-1ab  A and we
deduce that
a-1b-1ab
A and we
deduce that
a-1b-1ab  A
A 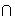 B = 1. Therefore
a-1b-1ab = 1, consequently ab = ba for all a
B = 1. Therefore
a-1b-1ab = 1, consequently ab = ba for all a  A and b
A and b  B. We can now define a map
B. We can now define a map
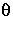 : A X B - > G
by
: A X B - > G
by
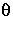 (a, b) = ab. Then
(a, b) = ab. Then
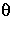 ((a1, b1)(a2, b2)) =
((a1, b1)(a2, b2)) = 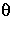 (a1a2, b1b2) = a1a2b1b2 = (a1b1)(a2b2)
(a1a2, b1b2) = a1a2b1b2 = (a1b1)(a2b2)
(because a2 commutes with b1), hence
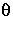 ((a1, b1)(a2, b2)) =
((a1, b1)(a2, b2)) = 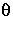 (a1, b1)
(a1, b1)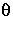 (a2, b2) and we deduce that
(a2, b2) and we deduce that 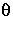 is a homomorphism. If
(a, b)
is a homomorphism. If
(a, b)  ker
ker 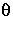 , then ab = 1 and so
a = b-1. Thus
a = b-1
, then ab = 1 and so
a = b-1. Thus
a = b-1  A
A 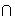 B = 1 and we deduce that a = b = 1. Therefore
ker
B = 1 and we deduce that a = b = 1. Therefore
ker 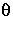 = 1 and so
= 1 and so 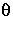 is a monomorphism. Since | G| = | A| X | B| we
conclude that
is a monomorphism. Since | G| = | A| X | B| we
conclude that 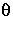 is also onto, consequently
is also onto, consequently 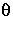 is an
isomorphism and the result follows.
is an
isomorphism and the result follows.
(ii)
Since A is a p-group, it has a normal subgroup P of order
p. Similarly B has a normal subgroup Q of order q.
Since P X Q is a normal subgroup of A X B of order
pq, we see that 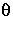 (P X Q) is a normal subgroup of
G of order pq, and so we may set N = P X Q to satisfy the
requirements of the problem.
(P X Q) is a normal subgroup of
G of order pq, and so we may set N = P X Q to satisfy the
requirements of the problem.
- 3.
- Let G be a simple group of order
22
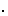 3
3 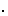 112.
The number of Sylow 11-subgroups is congruent to 1 modulo 11 and
divides 12, so the possibilities are 1 and 12. If there is 1 Sylow
11-subgroup, then it would have to be normal, which is not possible
because G is simple. Therefore there are 12 Sylow 11-subgroups. If
N is the normalizer of a Sylow 11-subgroup, then [G : N] is the
number of Sylow 11-subgroups, so
[G : N] = 12. By considering the
permutation representation of G on the left cosets of N in G and
using the fact that G is simple, we see that there is a monomorphism
of G into A12, the alternating group of degree 12. This means
that G is isomorphic to a subgroup of A12. This is not
possible because 121 divides | G|, but 121 does not divide | A12|.
We now have a contradiction and we deduce that no such G exists, as
required.
112.
The number of Sylow 11-subgroups is congruent to 1 modulo 11 and
divides 12, so the possibilities are 1 and 12. If there is 1 Sylow
11-subgroup, then it would have to be normal, which is not possible
because G is simple. Therefore there are 12 Sylow 11-subgroups. If
N is the normalizer of a Sylow 11-subgroup, then [G : N] is the
number of Sylow 11-subgroups, so
[G : N] = 12. By considering the
permutation representation of G on the left cosets of N in G and
using the fact that G is simple, we see that there is a monomorphism
of G into A12, the alternating group of degree 12. This means
that G is isomorphic to a subgroup of A12. This is not
possible because 121 divides | G|, but 121 does not divide | A12|.
We now have a contradiction and we deduce that no such G exists, as
required.
- 4.
- Since
(
 +
+ 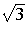 )3 - 9(
)3 - 9( +
+ 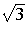 ) = 2
) = 2 , we see that
, we see that


 [
[ +
+ 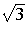 ] and we deduce that
] and we deduce that
 [
[ +
+ 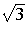 ] =
] =  [
[ ,
,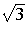 ]. Now
[
]. Now
[ [
[ ] :
] :  ] = 2, and
[
] = 2, and
[ [
[ ,
,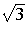 ] :
] :  [
[ ]] = 1 or 2, because
]] = 1 or 2, because 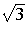 satisfies x2 - 3, a degree 2 polynomial over
satisfies x2 - 3, a degree 2 polynomial over
 . Therefore
[
. Therefore
[ [
[ +
+ 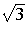 ] :
] :  ] = 4 or 2, depending on
whether or not
] = 4 or 2, depending on
whether or not
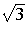

 [
[ ].
].
Suppose
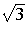

 [
[ ]. Then we may write
]. Then we may write
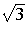 = a + b
= a + b where
a, b
where
a, b 
 . Clearly
a, b
. Clearly
a, b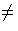 0. Squaring we obtain
3 = a2 + 2ab
0. Squaring we obtain
3 = a2 + 2ab + 2b2
and we deduce that
+ 2b2
and we deduce that  is rational, which is not so. Therefore
is rational, which is not so. Therefore
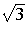
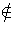
 [
[ ] and consequently
] and consequently
 [
[ +
+ 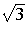 ] = 4. Note we also have
that
{1,
] = 4. Note we also have
that
{1, } is a
} is a
 -basis for
-basis for
 [
[ ], and
{1,
], and
{1,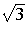 } is a
} is a
 [
[ ]-basis for
]-basis for
 [
[ ,
,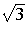 ].
Recall that if ei is an F-basis for E over F and fj is an
E-basis for K, then eifj is an F-basis for K.
It follows that
{1,
].
Recall that if ei is an F-basis for E over F and fj is an
E-basis for K, then eifj is an F-basis for K.
It follows that
{1, ,
,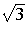 ,
,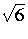 } is
a
} is
a
 -basis for
-basis for
 [
[ ,
,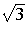 ].
].
- 5.
- Let P be a prime ideal of D and suppose P was not maximal.
Then there would exist M
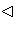 D such that M
D such that M D and M properly
containing P. Since D is a PID, we may write P = pD and M = mD for some m, p
D and M properly
containing P. Since D is a PID, we may write P = pD and M = mD for some m, p  D with p
D with p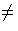 0.
Then p = mx for some x
0.
Then p = mx for some x  D because M
contains P. Since P is a prime ideal, we must have m or x
D because M
contains P. Since P is a prime ideal, we must have m or x  P. We cannot have m
P. We cannot have m  P because M properly contains P.
Therefore we must have x
P because M properly contains P.
Therefore we must have x  P and then we may write x = py for
some y
P and then we may write x = py for
some y  D. This yields p = mpy and since D is a domain, we
see that 1 = my. This shows that mD = D, which contradicts the
fact that M is a proper ideal of D and the first part of the
problem is proven.
D. This yields p = mpy and since D is a domain, we
see that 1 = my. This shows that mD = D, which contradicts the
fact that M is a proper ideal of D and the first part of the
problem is proven.
Suppose now that
f : D - > K is a ring epimorphism onto the
integral domain K with
kerf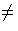 0. Then
D/kerf
0. Then
D/kerf 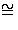 K, so
ker f is a prime ideal because D/ker f is an integral domain.
Using the first part of the problem, we see that ker f is a
maximal ideal of D. Therefore D/ker f is a field and it follows
that K is a field as required.
K, so
ker f is a prime ideal because D/ker f is an integral domain.
Using the first part of the problem, we see that ker f is a
maximal ideal of D. Therefore D/ker f is a field and it follows
that K is a field as required.
For the last part a counterexample is
R =  /6
/6 .
Let P be the prime ideal
2
.
Let P be the prime ideal
2 /6
/6 , Q the
prime ideal
3
, Q the
prime ideal
3 /6
/6 , and
S = R
, and
S = R 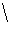 P.
Note that the ideals of R are precisely 0, R, P
and Q, and the prime ideals of R are precisely P and Q.
Then
S-1P = 0 because
s = 6
P.
Note that the ideals of R are precisely 0, R, P
and Q, and the prime ideals of R are precisely P and Q.
Then
S-1P = 0 because
s = 6 + 3
+ 3  S and sp = 0 for all p
S and sp = 0 for all p  P, and
S-1Q = RP because
Q
P, and
S-1Q = RP because
Q 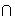 S
S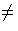
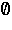 . Since all ideals of RP are
of the form S-1I for some I
. Since all ideals of RP are
of the form S-1I for some I 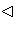 R, we see that 0 and RP are
the only ideals of RP and it follows that RP is a field.
Similarly RQ is a field. Since R is not an integral domain, we
have now established that R is a counterexample.
R, we see that 0 and RP are
the only ideals of RP and it follows that RP is a field.
Similarly RQ is a field. Since R is not an integral domain, we
have now established that R is a counterexample.
- 6.
- Suppose
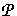 is a prime ideal of R and
R
is a prime ideal of R and
R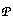 has a nonzero nilpotent element. Then we may assume that
R
has a nonzero nilpotent element. Then we may assume that
R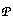 has a nonzero element
has a nonzero element 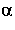 such that
such that
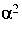 = 0. If
S = R
= 0. If
S = R 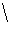
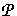 , then we may write the nilpotent element as r/s where
r
, then we may write the nilpotent element as r/s where
r  R and s
R and s  S. Since
(r/s)2 = 0, we see that r2t = 0 for some t
S. Since
(r/s)2 = 0, we see that r2t = 0 for some t  S, and rt
S, and rt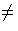 0 because r/s
0 because r/s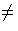 0. Also
(rt)2 = r2tt = 0, so rt is a nonzero nilpotent element of R.
0. Also
(rt)2 = r2tt = 0, so rt is a nonzero nilpotent element of R.
Suppose r is a nonzero nilpotent element of R. It remains to
prove that
R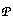 has a nonzero nilpotent element for some
prime ideal
has a nonzero nilpotent element for some
prime ideal
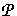 of R. We may assume that r2 = 0.
Let
I = {s
of R. We may assume that r2 = 0.
Let
I = {s  R | rs = 0} , an ideal of R which does not contain 1. By Zorn's lemma, there
is a maximal ideal
R | rs = 0} , an ideal of R which does not contain 1. By Zorn's lemma, there
is a maximal ideal
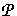 of R containing I; of course
of R containing I; of course
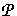 will also be a prime ideal. Then the image r/1 in
R
will also be a prime ideal. Then the image r/1 in
R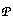 is nonzero because rt
is nonzero because rt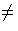 0 for all
t
0 for all
t  R
R 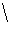
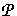 . Since
(r/1)2 = r2/12 = 0/12 = 0,
we see that r/1 is a nonzero nilpotent element of
R
. Since
(r/1)2 = r2/12 = 0/12 = 0,
we see that r/1 is a nonzero nilpotent element of
R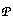 . This completes the proof.
. This completes the proof.
- 7.
- The submodule of M generated by A and B is A + B; this is
the set
{a + b | a
 A and b
A and b  B} . Thus we need to prove
that
A
B} . Thus we need to prove
that
A 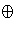 B
B 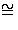 A + B. We define a map
A + B. We define a map
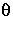 : A
: A 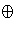 B - > M by
B - > M by
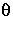 (a, b) = a + b. Clearly this is an R-module
homomorphism of
A
(a, b) = a + b. Clearly this is an R-module
homomorphism of
A 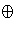 B onto A + B. If
(a, b)
B onto A + B. If
(a, b)  ker
ker 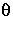 ,
then a + b = 0, consequently a = - b. This shows that a and - b
are both in
A
,
then a + b = 0, consequently a = - b. This shows that a and - b
are both in
A 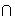 B = 0. Therefore a = b = 0 and hence
ker
B = 0. Therefore a = b = 0 and hence
ker 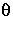 = 0. It follows that
= 0. It follows that 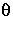 is an isomorphism and so
A
is an isomorphism and so
A 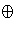 B
B 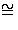 A + B as required.
A + B as required.
- 8.
- (i) Since there is a one-one correspondence between the subgroups of
Gal(E/F) (the Galois group of E over F) and the proper
subfields of E containing F, we need to show that S6 has at
least 35 proper subgroups. One way to do this is to note that S6
has 144 5-cycles which gives 36 subgroups of order 5.
(ii) The subfield L required is Fix(A6), the subset of E which
is fixed pointwise by all elements of the alternating subgroup A6
of S6. Since A6 is a normal subgroup of S6, we see that L
is a Galois extension of F, and that Gal
(E/L) 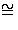 A6. Since
A6 is a simple group, there is no subfield between E and L
which is Galois over L.
A6. Since
A6 is a simple group, there is no subfield between E and L
which is Galois over L.
(iii) The dimension of L over F is
| S6/A6| = 2.
![]() ((a1, b1)(a2, b2)) =
((a1, b1)(a2, b2)) = ![]() (a1a2, b1b2) = a1a2b1b2 = (a1b1)(a2b2)
(a1a2, b1b2) = a1a2b1b2 = (a1b1)(a2b2)
![]() (P X Q) is a normal subgroup of
G of order pq, and so we may set N = P X Q to satisfy the
requirements of the problem.
(P X Q) is a normal subgroup of
G of order pq, and so we may set N = P X Q to satisfy the
requirements of the problem.
![]()
![]()
![]() [
[![]() ]. Then we may write
]. Then we may write
![]() = a + b
= a + b![]() where
a, b
where
a, b ![]()
![]() . Clearly
a, b
. Clearly
a, b![]() 0. Squaring we obtain
3 = a2 + 2ab
0. Squaring we obtain
3 = a2 + 2ab![]() + 2b2
and we deduce that
+ 2b2
and we deduce that ![]() is rational, which is not so. Therefore
is rational, which is not so. Therefore
![]()
![]()
![]() [
[![]() ] and consequently
] and consequently
![]() [
[![]() +
+ ![]() ] = 4. Note we also have
that
{1,
] = 4. Note we also have
that
{1,![]() } is a
} is a
![]() -basis for
-basis for
![]() [
[![]() ], and
{1,
], and
{1,![]() } is a
} is a
![]() [
[![]() ]-basis for
]-basis for
![]() [
[![]() ,
,![]() ].
Recall that if ei is an F-basis for E over F and fj is an
E-basis for K, then eifj is an F-basis for K.
It follows that
{1,
].
Recall that if ei is an F-basis for E over F and fj is an
E-basis for K, then eifj is an F-basis for K.
It follows that
{1,![]() ,
,![]() ,
,![]() } is
a
} is
a
![]() -basis for
-basis for
![]() [
[![]() ,
,![]() ].
].
![]() 0. Then
D/kerf
0. Then
D/kerf ![]() K, so
ker f is a prime ideal because D/ker f is an integral domain.
Using the first part of the problem, we see that ker f is a
maximal ideal of D. Therefore D/ker f is a field and it follows
that K is a field as required.
K, so
ker f is a prime ideal because D/ker f is an integral domain.
Using the first part of the problem, we see that ker f is a
maximal ideal of D. Therefore D/ker f is a field and it follows
that K is a field as required.
![]() /6
/6![]() .
Let P be the prime ideal
2
.
Let P be the prime ideal
2![]() /6
/6![]() , Q the
prime ideal
3
, Q the
prime ideal
3![]() /6
/6![]() , and
S = R
, and
S = R ![]() P.
Note that the ideals of R are precisely 0, R, P
and Q, and the prime ideals of R are precisely P and Q.
Then
S-1P = 0 because
s = 6
P.
Note that the ideals of R are precisely 0, R, P
and Q, and the prime ideals of R are precisely P and Q.
Then
S-1P = 0 because
s = 6![]() + 3
+ 3 ![]() S and sp = 0 for all p
S and sp = 0 for all p ![]() P, and
S-1Q = RP because
Q
P, and
S-1Q = RP because
Q ![]() S
S![]()
![]() . Since all ideals of RP are
of the form S-1I for some I
. Since all ideals of RP are
of the form S-1I for some I ![]() R, we see that 0 and RP are
the only ideals of RP and it follows that RP is a field.
Similarly RQ is a field. Since R is not an integral domain, we
have now established that R is a counterexample.
R, we see that 0 and RP are
the only ideals of RP and it follows that RP is a field.
Similarly RQ is a field. Since R is not an integral domain, we
have now established that R is a counterexample.
![]() has a nonzero nilpotent element for some
prime ideal
has a nonzero nilpotent element for some
prime ideal
![]() of R. We may assume that r2 = 0.
Let
I = {s
of R. We may assume that r2 = 0.
Let
I = {s ![]() R | rs = 0} , an ideal of R which does not contain 1. By Zorn's lemma, there
is a maximal ideal
R | rs = 0} , an ideal of R which does not contain 1. By Zorn's lemma, there
is a maximal ideal
![]() of R containing I; of course
of R containing I; of course
![]() will also be a prime ideal. Then the image r/1 in
R
will also be a prime ideal. Then the image r/1 in
R![]() is nonzero because rt
is nonzero because rt![]() 0 for all
t
0 for all
t ![]() R
R ![]()
![]() . Since
(r/1)2 = r2/12 = 0/12 = 0,
we see that r/1 is a nonzero nilpotent element of
R
. Since
(r/1)2 = r2/12 = 0/12 = 0,
we see that r/1 is a nonzero nilpotent element of
R![]() . This completes the proof.
. This completes the proof.
![]() A6. Since
A6 is a simple group, there is no subfield between E and L
which is Galois over L.
A6. Since
A6 is a simple group, there is no subfield between E and L
which is Galois over L.