ALGEBRA PRELIMINARY EXAMINATION:
Winter 2001
Do all problems. All rings should be assumed to have a 1.
- Let R, A and B be commutative rings with
R
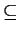 A and
R
A and
R 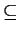 B. Prove that if A is an integral extension of R and
B is an integral extension of R, then the ring
A
B. Prove that if A is an integral extension of R and
B is an integral extension of R, then the ring
A 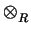 B is
also an integral extension of R.
B is
also an integral extension of R.
- For this problem all fields have characteristic 0. Let K/L be a
Galois extension with Galois group G and let H be a subgroup of
G. Prove that there exists some
b
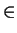 K such that
H coincides with
K such that
H coincides with
{
s 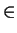 G
G |
s(
b) =
b}.
- Let S be a semisimple ring. Prove that S X S is semisimple.
- Let G be a finite group and assume that p is a fixed prime
divisor of its order. Set
K =
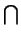 NG(P)
where the intersection is taken over all Sylow p-subgroups P of
G and
NG(
NG(P)
where the intersection is taken over all Sylow p-subgroups P of
G and
NG( ) denotes the normalizer. Show that
) denotes the normalizer. Show that
- (a)
- K
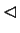 G.
G.
- (b)
- G and G/K have the same number of Sylow p-subgroups.
- Suppose A is an abelian group (written additively) of order pM
for some prime p. Prove that if n is a positive integer such
that pnA = 0, then
|{
a 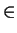 A
A |
pa = 0}|
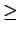 pM/n
pM/n.
- Let G be a finite group. Prove that if H and K are normal
nilpotent subgroups of G, then so is HK.
- Prove or disprove: let
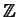 6
denote the ring of integers modulo 6. Then every projective
6
denote the ring of integers modulo 6. Then every projective
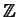 6-module is free.
6-module is free.
Peter Linnell
2001-02-16
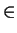 G | s(b) = b}.
G | s(b) = b}.
 G.
G.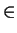 A | pa = 0}|
A | pa = 0}|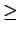 pM/n.
pM/n.