Since a group of prime power order has normal subgroups of order m
for all m dividing the
order of the group, we see that A has a normal subgroup
H of order 25. From the previous paragraph, B centralizes H and
so certainly normalizes H. Thus A and B normalize H, hence
| A| and | B| divide the order of the
normalizer of H in G and we conclude
that H ![]() G. This completes the solution.
G. This completes the solution.
- (a)
- Since D is a conjugacy class in f-1(C), we may write
D = {bdb-1 | b
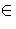 f-1(C)} for some fixed d
f-1(C)} for some fixed d 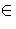 D. Then
D. Then
f (D) = {f (bdb-1) = f (b)f (d )f (b)-1 | b
Therefore f (D) = {cf (d )c-1 | c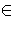 f-1(C)}.
f-1(C)}.
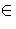 C} , and (a) follows.
C} , and (a) follows.
- (b)
- Let D(g) denote the conjugacy class of g in f-1(C).
Since f (g) is centralized by C, the conjugacy class containing
f (g) is precisely {f (g)} . Since f (D(g)) is by (a) the conjugacy
class containing f (g), we see that
| f (D(g))| = 1. Therefore all
elements of D(g) are in the same coset of ker f and we conclude
that
| D(g)|
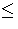 | ker f| as required.
| ker f| as required.
- (c)
- Let K denote the centralizer of g in f-1(C). Then the
order of the centralizer of g in G is at least | K|. Now the
order of the conjugacy class of g in f-1(C) is
[f-1(C) : K], and by (b) this order is at most
| ker f|. Therefore
[f-1(C) : K]
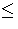 | ker f|, consequently
| ker f|, consequently
| K|
because f-1(C)/ker f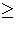 | f-1(C)/ker f| = | C|
| f-1(C)/ker f| = | C|
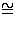 C. The result follows.
C. The result follows.
- (a)
- If R has no prime elements, then R is a field and so
certainly a PID. Therefore we may suppose that R has exactly one
prime p (up to a multiple of a unit), and we need to prove that R is a
PID. Let I be a nonzero ideal of R. Then each nonzero element of
I can be written in the form upn for some nonnegative integer n
and some unit u, because p is the only prime (up to a multiple of
a unit) of R. Let N be the smallest nonnegative integer such that
upN
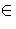 I for some unit u. We now show that I = pNR; clearly
pNR
I for some unit u. We now show that I = pNR; clearly
pNR 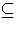 I. If
x
I. If
x 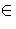 I
\ 0, then we may
write x = vpn for some unit v and
some integer n
I
\ 0, then we may
write x = vpn for some unit v and
some integer n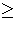 N. Thus
x = pNvpn - N
which shows that
x
N. Thus
x = pNvpn - N
which shows that
x 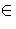 pNR, and the result follows.
pNR, and the result follows.
- (b)
- Suppose every maximal ideal of R is principal. Then each
maximal ideal of R is of the form pR where p is a prime of R.
Suppose by way of contradiction that I is a nonprincipal ideal of
R. Clearly
0
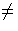 I
I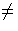 R. Choose a nonzero element x
R. Choose a nonzero element x 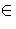 I,
and write
x = p1d1... pndn, where the pi are
nonassociate primes and the di are positive integers.
I,
and write
x = p1d1... pndn, where the pi are
nonassociate primes and the di are positive integers.
For each prime p, let e(p) denote the largest integer such that pe(p)R
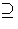 I. If p is not an associate of one of the
pi, then e(p) = 0. Set
y = p1e1... pnen. We
claim that I = yR.
I. If p is not an associate of one of the
pi, then e(p) = 0. Set
y = p1e1... pnen. We
claim that I = yR.
First we show that I
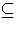 yR. If z
yR. If z 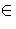 I,
then by unique factorization we may write
z = qp1f1... pnfn, where the fi are nonnegative
integers and q is a product of primes which are not associate to
any of the pi. Again using unique factorization, we must have
fi
I,
then by unique factorization we may write
z = qp1f1... pnfn, where the fi are nonnegative
integers and q is a product of primes which are not associate to
any of the pi. Again using unique factorization, we must have
fi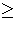 ei for all i and we deduce that z
ei for all i and we deduce that z 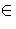 yR.
yR.
Finally we show that yR
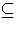 I. Set
J = {r
I. Set
J = {r 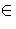 R | yr
R | yr 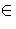 I} (so
J = y-1I). Clearly J is an ideal of R and yJ = I. If J
I} (so
J = y-1I). Clearly J is an ideal of R and yJ = I. If J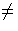 R, then by Zorn's lemma J is
contained in a maximal ideal of R, which we may assume is of the
form pR where p is a prime of R. It would follow that
ypR
R, then by Zorn's lemma J is
contained in a maximal ideal of R, which we may assume is of the
form pR where p is a prime of R. It would follow that
ypR 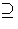 I, which contradicts the maximality of the e(p).
Therefore J = R and we deduce that
yR
I, which contradicts the maximality of the e(p).
Therefore J = R and we deduce that
yR 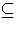 I. Thus I = yR
and the proof is complete.
I. Thus I = yR
and the proof is complete.
0 ![]() N
N![]()
![]() M
M ![]() M/N
M/N ![]() 0
0