. Let H be a subgroup of G of order 27. Up
to isomorphism, describe H.
Qualifying Examination Algebra Fall 1995
#1. Suppose that G is a group of order (35)3. Show that G has normal Sylow 5- and 7-subgroups. Also show that G has a normal subgroup of order 25.
#2. Suppose that G is an abelian group isomorphic to
. Let H be a subgroup of G of order 27. Up
to isomorphism, describe H.
#3. Let 
be a group epimorphism with G finite,
let 
, and let C denote the centralizer of f(g) in H.
a). Prove that if D is a conjugacy class in f-1(C), then f(D) is a conjugacy class in C.
b). Prove that the order of the conjugacy class of g in
f-1(C) is at most 
.
c). Prove that the order of the centralizer of g in G is at least |C|.
#4. Suppose that R is a unique factorization domain which is NOT a principal ideal domain.
a). Show that R must have at least two (nonassociate) prime elements.
b). Show that R must have a nonprincipal maximal ideal.
#5. Let R be a ring with a 1 and suppose that X is an
R-module and N is a submodule
of an R-module M. Let 
denote the inclusion
map and let 
be the R-module homomorphism 
.
Prove that if
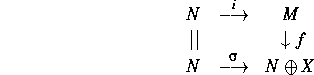
is a commutative diagram
for some R-homomorphism f, then M is isomorphic
to 
.
#6. Suppose that E is a Galois field extension of F with
[E:F]=pn for some prime p and positive integer n. Show that
there are intermediate fields 
so that [Ki:Ki-1] = p and Ki
is Galois over F for i =1, ... , n.
#7. Prove that there is no finite field which is algebraically closed.