- (i)
- By definition
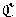 (x) = {gxg-1 | g
(x) = {gxg-1 | g  G} .
Since
x
G} .
Since
x  H
H  G, we see that
gxg-1
G, we see that
gxg-1  H for all g
H for all g  G and we deduce that
G and we deduce that
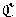 (x)
(x) 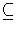 H. Let CG(x)
denote the centralizer of x in G. Then
|
H. Let CG(x)
denote the centralizer of x in G. Then
|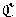 (x)| = [G : CG(x)]. This last quantity is a power
of p and it cannot be 1 because x is not in the center of G. We
deduce that
|
(x)| = [G : CG(x)]. This last quantity is a power
of p and it cannot be 1 because x is not in the center of G. We
deduce that
|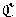 (x)| is a nontrivial power of p and
(i) follows.
(x)| is a nontrivial power of p and
(i) follows.
- (ii)
- It follows from (i) that
H
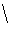 Z is a union of conjugacy
classes of the form
Z is a union of conjugacy
classes of the form
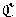 (x) where
x
(x) where
x  H
H 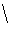 Z.
Since different conjugacy classes intersect trivially, we see from (i)
that p divides
| H
Z.
Since different conjugacy classes intersect trivially, we see from (i)
that p divides
| H 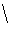 Z|. Also | H| divides | G| and so
| H| is a nontrivial power of p. We deduce that p divides
| Z
Z|. Also | H| divides | G| and so
| H| is a nontrivial power of p. We deduce that p divides
| Z 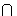 H| and (ii) is proven.
H| and (ii) is proven.
- (iii)
- Let H be the centralizer of A in G. Then H is a normal
subgroup of G containing A and it will be sufficient to show that
H = A. Let X/A be the center of G/A and suppose H > A. Then
we see from (ii) that
X/A
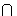 H/A > 1 because
H/A
H/A > 1 because
H/A 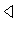 G/A,
and we deduce that there is
a nontrivial cyclic subgroup Y/A contained in
X/A
G/A,
and we deduce that there is
a nontrivial cyclic subgroup Y/A contained in
X/A 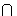 H/A. Since
Y/A
H/A. Since
Y/A 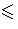 X/A we see that
Y/A
X/A we see that
Y/A 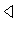 G and we deduce that
Y
G and we deduce that
Y 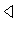 G. Also A is contained in the center of Y and Y/A is
cyclic, hence Y is abelian. This contradicts the fact that A is
a maximal normal abelian subgroup of G and the result follows
G. Also A is contained in the center of Y and Y/A is
cyclic, hence Y is abelian. This contradicts the fact that A is
a maximal normal abelian subgroup of G and the result follows
- (i)
- The number of Sylow 5-subgroups of G divides 36 and is congruent to 1 modulo 5, which means that this number must be 1,6 or 36. It cannot be 1, for then G would have a normal Sylow 5-subgroup, which contradicts the fact that G is simple. Nor can G have 6 Sylow 5-subgroups, for then G would be isomorphic to a subgroup of A6 because G is simple. This would mean that A6 has a subgroup of index 2, and since subgroups of index 2 are always normal, this would contradict the fact that A6 is simple. We conclude that G has 36 Sylow 5-subgroups.
- (ii)
- Let N be the normalizer of a Sylow 3-subgroup. Then the number of Sylow 3-subgroups is [G : N]. Also the number of Sylow 3-subgroups divides 20 and is congruent to 1 modulo 3, so this number is 1,4 or 10. It cannot be 1 because that would mean G has a normal Sylow 3-subgroup, which would contradict the fact that G is simple. Nor can it be 4, for then G would be isomorphic to a subgroup of A4 because G is simple, which is clearly impossible. Therefore the number of Sylow 3-subgroups is 10. We deduce that [G : N] = 10 and hence N has order 18.
- (iii)
- A Sylow 3-subgroup of a group of order 18 has order 9. This means the subgroup has index 2, hence the subgroup is normal because in any group, a subgroup of index 2 is normal.
- (d)
- Let C be the centralizer in G of A
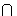 B and suppose A
B and suppose A 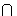 B is not 1. Then C contains A, B and A
B is not 1. Then C contains A, B and A 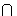 B is a normal
subgroup in C, so C cannot be the whole of G. Therefore the
order of C is a multiple of 9 and divides 180, and is neither 9 nor
180. Let d be the index of C in G, so
| C| = | G|/d.
Then G is isomorphic to a
subgroup of Ad because G is simple. Since the order of Ad is
less than 180 if d
B is a normal
subgroup in C, so C cannot be the whole of G. Therefore the
order of C is a multiple of 9 and divides 180, and is neither 9 nor
180. Let d be the index of C in G, so
| C| = | G|/d.
Then G is isomorphic to a
subgroup of Ad because G is simple. Since the order of Ad is
less than 180 if d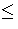 5, we see that d
5, we see that d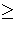 6 and consequently
C has order 18. From part (iii), the Sylow 3-subgroup of C is
normal in C and therefore C has exactly one subgroup of order 9.
We now have a contradiction because C has two subgroups of order 9,
namely A and B. We conclude that
A
6 and consequently
C has order 18. From part (iii), the Sylow 3-subgroup of C is
normal in C and therefore C has exactly one subgroup of order 9.
We now have a contradiction because C has two subgroups of order 9,
namely A and B. We conclude that
A 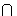 B = 1.
B = 1.
- (e)
- We count the elements in G. Since two Sylow 5-subgroups intersect in 1 and there are 36 Sylow 5-subgroups by (i), we see that G has 36*4 = 144 elements of order 5. Also two Sylow 3-subgroups intersect in 1 by (iv) and G has 10 Sylow 3-subgroups by (ii). Therefore G has 8*10 = 80 elements of order 3 or 9. We conclude that G has at least 144 + 80 = 224 elements, which contradicts the fact that G has only 180 elements. It follows that no such G can exist and thus there is no simple group of order 180.
Since rM = 0, we see that
rR ![]() sR and hence s divides
r. Suppose there do not exist distinct primes p, q dividing r.
Then the same is true for s because s divides r, and we deduce
that s is a prime power, say pe for some prime p. From the
uniqueness statement in the fundamental structure theorem for finitely
generated modules over a PID, we cannot write
R/Rpe = A
sR and hence s divides
r. Suppose there do not exist distinct primes p, q dividing r.
Then the same is true for s because s divides r, and we deduce
that s is a prime power, say pe for some prime p. From the
uniqueness statement in the fundamental structure theorem for finitely
generated modules over a PID, we cannot write
R/Rpe = A ![]() B
where A, B are nonzero R-modules and we have a contradiction. This
finishes the proof.
B
where A, B are nonzero R-modules and we have a contradiction. This
finishes the proof.
- (i)
- Choose integers r, s such that
qr + 2s = 1.
Then in
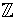 [[X]]/(X - 2) we have
qr = 1 - sX mod (X - 2).
Since 1 - sX is
invertible in
[[X]]/(X - 2) we have
qr = 1 - sX mod (X - 2).
Since 1 - sX is
invertible in
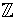 [[X]] (with inverse
1 + sX + s2X2 + ...), it follows that q is invertible in
[[X]] (with inverse
1 + sX + s2X2 + ...), it follows that q is invertible in
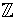 [[X]]/(X - 2).
[[X]]/(X - 2).
- (ii)
- The general element of R is
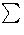 aiXi mod (X - 2), where
ai
aiXi mod (X - 2), where
ai 
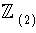 for all i. Now each ai is of the
form p/q where
p, q
for all i. Now each ai is of the
form p/q where
p, q 
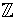 and q is odd. Using (i), we
may now write ai = bi mod (X - 2)
where
bi
and q is odd. Using (i), we
may now write ai = bi mod (X - 2)
where
bi 
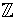 [[X]], and then we may write the
general element of R in the form
[[X]], and then we may write the
general element of R in the form
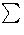 biXi mod
(X - 2). This proves that
biXi mod
(X - 2). This proves that
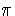
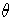 is surjective. We now determine
the kernel of
is surjective. We now determine
the kernel of
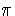
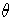 . Obviously
(X - 2)
. Obviously
(X - 2) 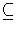 ker
ker 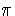
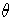 . Conversely suppose
f
. Conversely suppose
f  ker
ker 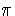
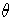 . Then we
may write
f = (X - 2)g where
g
. Then we
may write
f = (X - 2)g where
g 
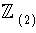 [[X]]. We want to
show that
g
[[X]]. We want to
show that
g 
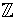 [[X]]. Write
g =
[[X]]. Write
g = 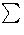 giXi where
gi
giXi where
gi 
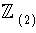 . Then the coefficient of Xn in g(X - 2)
is
gn - 1 - 2gn for n > 0, and the constant coefficient is
-2g0. By induction on n we see that
2gn
. Then the coefficient of Xn in g(X - 2)
is
gn - 1 - 2gn for n > 0, and the constant coefficient is
-2g0. By induction on n we see that
2gn 
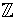 and since
gn
and since
gn 
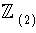 , we conclude that
gn
, we conclude that
gn 
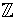 for all n. This proves that
ker
for all n. This proves that
ker 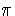
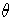 = (X - 2)
and it now follows from the fundamental isomorphism theorem that
R
= (X - 2)
and it now follows from the fundamental isomorphism theorem that
R 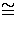
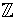 [[X]]/(X - 2).
[[X]]/(X - 2).
- (iii)
- By considering the homomorphism
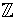 [X]
[X]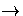
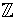 determined by sending X to 2,
we see that
determined by sending X to 2,
we see that
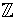 [X]/(X - 2)
[X]/(X - 2) 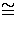
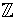 . Since 3 is not invertible in
. Since 3 is not invertible in
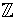 , we see that
3 is not invertible in
, we see that
3 is not invertible in
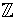 [X]/(X - 2). But 3 is invertible in R
and the result follows.
[X]/(X - 2). But 3 is invertible in R
and the result follows.
- (i)
- Obviously
K(
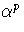 )
) 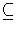 K(
K( ). Also
). Also  is
separable over
K(
is
separable over
K(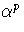 ) and satisfies the polynomial
Xp -
) and satisfies the polynomial
Xp - 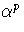 . Since
. Since  is the only root of
Xp -
is the only root of
Xp -  , it
follows that
, it
follows that

 K(
K(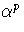 ) and hence
K(
) and hence
K( ) = K(
) = K(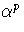 ).
Now we consider the minimum polynomial of
).
Now we consider the minimum polynomial of 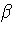 over K. This has
degree p because
[K(
over K. This has
degree p because
[K(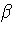 ) : K] = p, and must be a polynomial
in Xp because
) : K] = p, and must be a polynomial
in Xp because 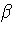 is not separable over K. Thus the minimum
polynomial must be of the form Xp - b for some b
is not separable over K. Thus the minimum
polynomial must be of the form Xp - b for some b  K and it
follows that
K and it
follows that
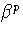 = b
= b  K.
K.
- (ii)
- Since we are in characteristic p, we have
(
 +
+ 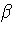 )p =
)p = 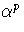 +
+ 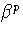 . But
. But
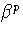
 K by (i), hence
K by (i), hence
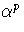
 K(
K( +
+ 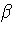 ). Therefore
K(
). Therefore
K(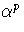 )
) 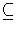 K(
K( +
+ 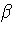 ) and it now follows from (i) that
K(
) and it now follows from (i) that
K( )
) 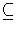 K(
K( +
+ 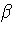 ) as required.
) as required.
- (iii)
- Since
K(
 +
+ 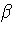 )
) 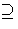 K(
K( ) by (ii), we have
[K(
) by (ii), we have
[K( +
+ 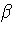 ) : K] = [K(
) : K] = [K( +
+ 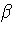 ) : K(
) : K( )][K(
)][K( ) : K] and since
[K(
) : K] and since
[K( ) : K] = d, it remains
to prove that
[K(
) : K] = d, it remains
to prove that
[K( +
+ 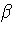 ) : K(
) : K( )] = p. Now
(
)] = p. Now
( +
+ 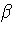 )p =
)p = 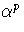 +
+ 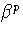
 K(
K( ) which shows that
[K(
) which shows that
[K( +
+ 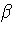 ) : K(
) : K( )] = p or 1, because we are in
characteristic p. It remains to prove that
[K(
)] = p or 1, because we are in
characteristic p. It remains to prove that
[K( +
+ 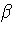 ) : K(
) : K( )]
)] 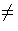 1, or
equivalently that
1, or
equivalently that
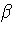
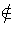 K(
K( ). But
). But  is
separable over K, hence every element of K(
is
separable over K, hence every element of K( ) is separable
over K which shows that
) is separable
over K which shows that
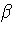
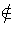 K(
K( ) because
) because 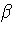 is
not separable over K. This completes the proof.
is
not separable over K. This completes the proof.
- (i)
- It will be sufficient to prove that Xp - t is irreducible in
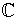 [t, X], or equivalently that t - Xp is irreducible
in
[t, X], or equivalently that t - Xp is irreducible
in
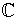 [X, t]. Let
R =
[X, t]. Let
R = 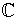 [X] and let
F =
[X] and let
F = 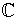 (X), the field of fractions of R. Then t - Xp is a monic
polynomial in R[t] and is irreducible in F[t], hence it is
irreducible in
R[t] =
(X), the field of fractions of R. Then t - Xp is a monic
polynomial in R[t] and is irreducible in F[t], hence it is
irreducible in
R[t] = 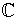 [X, t] and the result follows.
[X, t] and the result follows.
- (ii)
- Let y be one of the roots of Xp - t in L. Since Xp - t
is irreducible in K[X], we see that
[K(y) : K] = p. Also the
roots of Xp - t are
e2n
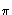 i/py where
n = 0,..., p - 1,
and since
e2n
i/py where
n = 0,..., p - 1,
and since
e2n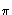 i/p
i/p 
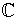 for all n, we deduce
that all the roots of Xp - t are in K(y). It follows that K(y) = L and we conclude that
[L : K] = p. Therefore the Galois group of
L over K has order p (note that L/K is a separable extension
because we are in characteristic zero). Since groups of order p are
cyclic, we conclude that the Galois group of L over K is cyclic of
order p and hence isomorphic to
for all n, we deduce
that all the roots of Xp - t are in K(y). It follows that K(y) = L and we conclude that
[L : K] = p. Therefore the Galois group of
L over K has order p (note that L/K is a separable extension
because we are in characteristic zero). Since groups of order p are
cyclic, we conclude that the Galois group of L over K is cyclic of
order p and hence isomorphic to
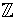 /p
/p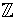 .
.