Algebra Preliminary Exam, Fall 1993
Do all problems
- 1.
- Assume that R is a ring and e
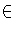 R has the property that
e2 = e. Prove that Re is a projective left R-module.
R has the property that
e2 = e. Prove that Re is a projective left R-module.
- 2.
- Let F be a field of characteristic zero and let K be a
finite field extension of F.
- (a)
- Explain why there is a polynomial
p(X)
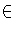 F[X] such that
K
F[X] such that
K 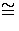 F[X]/(p).
F[X]/(p).
- (b)
- Prove that if
c
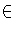 K[X]/(p) and c2 = 0, then c = 0.
K[X]/(p) and c2 = 0, then c = 0.
- 3.
- Let M
2(
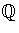 ) denote the group of 2 X 2 matrices
with rational entries under addition,
and let GL
2(
) denote the group of 2 X 2 matrices
with rational entries under addition,
and let GL
2(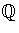 ) denote
the group of invertible 2 X 2 matrices with rational entries
under multiplication.
) denote
the group of invertible 2 X 2 matrices with rational entries
under multiplication.
- (a)
- Prove that if M
2(
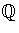 ) acts on a set, then all
orbits are either infinite or singletons.
) acts on a set, then all
orbits are either infinite or singletons.
- (b)
- Show that GL
2(
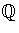 ) acts on
) acts on
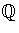 via
g*l
= det(g)l / | det (g)|, and that there exists a finite
orbit which is not a singleton.
via
g*l
= det(g)l / | det (g)|, and that there exists a finite
orbit which is not a singleton.
- 4.
- Let G be the direct product of the dihedral group of order 34
and the cyclic group of order 9. Suppose that L is a field and G
is a group of automorphisms of L. Prove that there is a unique
field K such that
LG
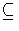 K and dimKL = 17. (You may
assume that charL = 0.)
K and dimKL = 17. (You may
assume that charL = 0.)
- 5.
- Let S be a commutative integral domain. Prove that if every
prime ideal of S[X] is principal, then S is a field.
- 6.
- Let A be an abelian group.
- (a)
- Show that the collection H of all homomorphisms from A to
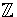 is a group under addition of functions.
is a group under addition of functions.
- (b)
- Prove that if
f1,..., fm
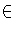 H, then the subgroup
generated by
f1,..., fm is free (i.e. free as a
H, then the subgroup
generated by
f1,..., fm is free (i.e. free as a
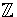 -module).
-module).
- 7.
- Let p be a prime, and let
G be the group of invertible 2 X 2 matrices under
multiplication with entries in the field of integers modulo p. Let
H be the subgroup consisting of all matrices of the form
- (a)
- Show that
| G| = (p2 - 1)(p2 - p).
- (b)
- Find all values of p such that the number of conjugates of
H in G is congruent to 8 mod p.
Return to
Peter Linnell
1999-05-31
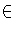 F[X] such that
K
F[X] such that
K 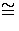 F[X]/(p).
F[X]/(p).
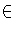 K[X]/(p) and c2 = 0, then c = 0.
K[X]/(p) and c2 = 0, then c = 0.
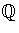 ) acts on a set, then all
orbits are either infinite or singletons.
) acts on a set, then all
orbits are either infinite or singletons.
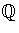 ) acts on
) acts on
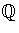 via
g*l
= det(g)l / | det (g)|, and that there exists a finite
orbit which is not a singleton.
via
g*l
= det(g)l / | det (g)|, and that there exists a finite
orbit which is not a singleton.
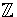 is a group under addition of functions.
is a group under addition of functions.
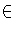 H, then the subgroup
generated by
f1,..., fm is free (i.e. free as a
H, then the subgroup
generated by
f1,..., fm is free (i.e. free as a
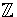 -module).
-module).