Algebra Prelim, Fall 1992

Answer all questions

1. Prove that any group of order 765 is abelian.
2. Let G be a finite group and let N be a normal subgroup of G. Prove that G is solvable if and only if both N and G/N are solvable.
3. 1. Prove that if G is a subgroup of S_n, then either 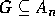or .
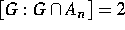   2. Prove that if 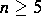and G is a normal subgroup of S_n, then 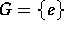, A_n or S_n.
   3. Prove that if 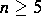, then S_n has no subgroup of index 3.
4. Let f(x) be an irreducible polynomial over with splitting field K. If the Galois group of is abelian, prove that for any roots of f(x) in K, we have .
5. Let K be a field and be a separable irreducible polynomial of degree 4, and let E be a splitting field for f(x) over K. If is a root of f(x) and , prove that there exists a subfield F of L with [F:K] = 2 if and only if the Galois group of E/K is not isomorphic to either A₄ or S₄.
6. 1. If G, H and K are finitely generated abelian groups with 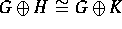, prove that .
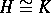   2. Give an example to show that part (a) is false if G is not finitely generated.
7. Let R be an integral domain. A nonzero element of R is a prime if implies that either or . A nonzero element is irreducible if implies that either a or b is a unit.
   1. Prove that every prime is irreducible.
   2. If R is a UFD, prove that every irreducible is prime.
8. Let R be a commutative ring with a 1, and let M be a cyclic R-module.
   1. Prove that M is isomophic to R/I for some ideal I of R.
   2. If N is any R-module, prove that 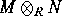is isomorphic to N/IN for some ideal I of R.

Return to

• Algebra Prelims Index
• Peter Linnell's Homepage

 
• About this document ...