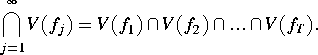![]()
- R is a local ring.
- R is integrally closed in K.
![]()
Prove that if f1,f2, ... is a countable list of polynomials in k[X1, ... ,Xn], then there is a positive integer T such that
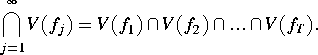
Algebra Qualifying Exam, Fall 1989
Do six problems
![]()
![]()
Prove that if f1,f2, ... is a countable list of polynomials in k[X1, ... ,Xn], then there is a positive integer T such that