Algebra Preliminary Exam, Fall 1988

Instructions: do all problems

1. Prove that there are no simple groups of order 600.
2. Let R be a principal ideal domain and assume that A, B, and C are finitely generated R-modules. Suppose that is isomorphic to . Prove that B is isomorphic to C.
3. Prove that the Galois group of a splitting field K of an irreducible polynomial p over the rational numbers acts transitively on the roots of p. Show by examples that this theorem does not necessarily hold if either
   1. K is not a splitting field, or
   2. p is reducible over .
4. Prove that a group of order 255 is cyclic.
5. Define what is meant by a solvable group. Prove that if , and H and G/H are solvable, then G is solvable.
6. Let be a linear map where V is a finite dimensional vector space over an algebraically closed field. Prove that if 0 is the only eigenvalue of T, then Tⁿ = 0 where .
7. Prove that if is a homomorphism between simple R-modules S and T, then either f is an isomorphism or f is the zero homomorphism. (Recall that a nonzero R-module is simple if 0 and the module itself are the only submodules.)
8. Let R be a commutative ring with a 1.
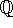   1. Prove that if M is a cyclic R-module, then M is isomorphic to R/I for some ideal I of R.
   2. Prove that if M is a cyclic R-module and N is an arbitrary R-module, then 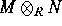is isomorphic to N/IN for some ideal I of R.

Return to

• Algebra Prelims Index
• Peter Linnell's Homepage

 
• About this document ...