- Let
A = P
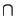 Q and
suppose A > 1. Since
P, Q
Q and
suppose A > 1. Since
P, Q 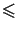 CG(A), we see that
P < CG(A). Using Lagrange's theorem, we deduce that
| CG(A)| = 96, 160 or 480. We cannot have 480 because then A would be a
central and hence a normal subgroup of G, which would contradict the
hypothesis that G is simple. Also we cannot have
| CG(A)| = 96
or 160, because that would mean that G has a subgroup of index 5 or
3. We now have a contradiction, and we conclude that A = 1.
CG(A), we see that
P < CG(A). Using Lagrange's theorem, we deduce that
| CG(A)| = 96, 160 or 480. We cannot have 480 because then A would be a
central and hence a normal subgroup of G, which would contradict the
hypothesis that G is simple. Also we cannot have
| CG(A)| = 96
or 160, because that would mean that G has a subgroup of index 5 or
3. We now have a contradiction, and we conclude that A = 1.
- The number of Sylow 2-subgroups is congruent to 1 modulo 2 and
divides 15. It cannot be 1 because that would mean that G has a
normal Sylow 2-subgroup. Nor can it be 3 or 5, because then G would
have a subgroup of index 3 or 5. Therefore G has 15 Sylow
2-subgroups. Next the number of Sylow 3-subgroups is congruent to 1
modulo 3 and divides 96. This number cannot be 1, because that would
mean that the Sylow 3-subgroup is normal. Nor can it be 4, because
that would yield a subgroup of index 4. Therefore G has at least 10
Sylow 3-subgroups. Finally the number of Sylow 7-subgroups is
congruent to 1 modulo 7 and divides 160. This number cannot be 1,
because that would mean that the Sylow 7-subgroup is normal.
Therefore G has at least 8 Sylow 7-subgroups.
We now count elements. Since by (a) any two Sylow 2-subgroups intersect trivially, there are 15*31 nontrivial elements whose order is a power of 2. Next any two Sylow 3-subgroups intersect trivially, because a Sylow 3-subgroup has prime order 3, and we see that there are at least 10*2 elements of order 3. Finally any two Sylow 5-subgroups intersect trivially, because a Sylow 5-subgroup has prime order 5, and we deduce that G has at least 6*4 elements of order 5. We now count elements: we find that G has at least 15*31 + 10*2 + 6*4 = 509 nontrivial elements. Since G has only 480 elements altogether, we have now arrived at a contradiction. We conclude that there is no such group G.
P 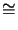
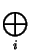 k[X]/(fi) and Q
k[X]/(fi) and Q 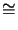
 k[X]/(gi)
k[X]/(gi)
where the fi, gi are either 0 or positive powers of
monic irreducible polynomials. Then we have
| Class Size | 1 | 6 | 8 | 6 | 3 |
| Class Rep | (1) | (12) | (123) | (1234) | (12)(34) |
| c1 | 1 | 1 | 1 | 1 | 1 |
| c2 | 1 | -1 | 1 | -1 | 1 |
| c3 | 2 | 0 | -1 | 0 | 2 |
| c4 | 3 | -1 | 0 | 1 | -1 |
| c5 | 3 | 1 | 0 | -1 | -1 |
| r | 4 | 2 | 1 | 0 | 0 |