Algebra Prelim, August 1999
Answer all questions
- Let G be a simple group of order 480 with an abelian Sylow
2-subgroup.
- If P and Q are distinct Sylow 2-subgroups of G,
by considering
CG(P
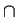 Q), prove that
P
Q), prove that
P 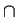 Q = 1.
Q = 1.
- Prove that there is no such group G.
- Let R be a UFD, let S be a multiplicatively closed subset
of R such that
0
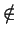 S, and let p be a prime in R. Prove
that p/1 is either a prime or a unit in S-1R.
S, and let p be a prime in R. Prove
that p/1 is either a prime or a unit in S-1R.
- Let k be the field
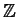 /2
/2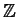 . Classify the
finitely generated projective
k[X]/(X3 + X)-modules up to
isomorphism.
. Classify the
finitely generated projective
k[X]/(X3 + X)-modules up to
isomorphism.
- Let R be a ring, let M be a Noetherian R-module, and let
J denote the Jacobson radical of R. Prove that either MJn = 0
for some positive integer n, or
MJn + 1
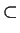 MJn (strict
inequality) for all positive integers n.
MJn (strict
inequality) for all positive integers n.
- Let R be a nonzero right Artinian ring (with a 1)
with no nonzero nilpotent
ideals and no nontrivial (
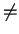 0, 1) idempotents.
Prove that R is a division ring.
0, 1) idempotents.
Prove that R is a division ring.
- Compute the character table of S4.
- Let K be a splitting field of the polynomial X4 - 2 over
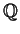 . Determine the order of
Gal(K/
. Determine the order of
Gal(K/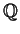 ). Use
this to show that K contains a subfield L such that
[L :
). Use
this to show that K contains a subfield L such that
[L : 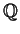 ] = 4 and L is normal over
] = 4 and L is normal over
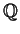 .
.
Peter Linnell
1999-08-12
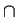 Q), prove that
P
Q), prove that
P 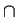 Q = 1.
Q = 1.