Algebra Prelim, August 1997
Answer all questions
- Let R be a commutative ring with unity and let I, J be ideals
of R.
- Prove that the product
IJ = {x
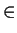 R | x = Si = 1naibi with ai
R | x = Si = 1naibi with ai 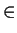 I and
bi
I and
bi 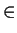 J} is an ideal of R.
J} is an ideal of R.
- Prove that
IJ
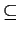 I
I 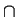 J.
J.
- If I + J = R, prove that
IJ = I
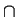 J.
J.
- If
IJ = I
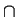 J for all ideals of R and R is an integral
domain, prove that R is a
field. (Hint: let I = Ra where a
J for all ideals of R and R is an integral
domain, prove that R is a
field. (Hint: let I = Ra where a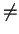 0 be a principal ideal
or R.)
0 be a principal ideal
or R.)
- Let F be a finite Galois extension of the field K with
Gal(F/K)
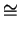 S5.
S5.
- Show that there are more than 40 fields strictly between F and
K.
- Show that there is a unique proper subfield E of F with E
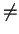 K such that E/K is a Galois extension. Determine [E : K] and
describe
Gal(E/K) up to isomorphism.
K such that E/K is a Galois extension. Determine [E : K] and
describe
Gal(E/K) up to isomorphism.
- Let G be a group of order 455.
- Prove that G is not simple.
- Prove that G is cyclic.
- Let R be a PID, let n be a positive integer, and let A and
B be finitely generated R-modules. If
An
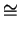 Bn, prove that
A
Bn, prove that
A 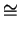 B. (An denotes the direct sum of n copies of A.)
B. (An denotes the direct sum of n copies of A.)
- Let P be a finitely generated projective
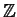 -module.
If P is also injective, prove that P = 0.
-module.
If P is also injective, prove that P = 0.
- Let A, B be abelian groups, and let m be a positive integer.
Prove that
A
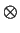 (B/mB)
(B/mB) 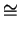 (A
(A 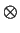 B)/m(A
B)/m(A 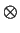 B).
B).
- Prove that a group of order 588 is solvable.
- Let
K =
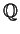 (
(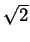 +
+ 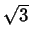 ,
,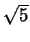 ).
).
- Determine
[K :
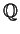 ].
].
- Compute
Gal(K/
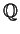 ).
).
Peter Linnell
1999-06-16
 R | x = Si = 1naibi with ai
R | x = Si = 1naibi with ai 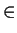 I and
bi
I and
bi 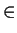 J} is an ideal of R.
J} is an ideal of R.
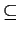 I
I 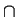 J.
J.
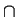 J.
J.
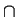 J for all ideals of R and R is an integral
domain, prove that R is a
field. (Hint: let I = Ra where a
J for all ideals of R and R is an integral
domain, prove that R is a
field. (Hint: let I = Ra where a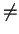 0 be a principal ideal
or R.)
0 be a principal ideal
or R.)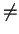 K such that E/K is a Galois extension. Determine [E : K] and
describe
Gal(E/K) up to isomorphism.
K such that E/K is a Galois extension. Determine [E : K] and
describe
Gal(E/K) up to isomorphism.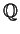 ].
].
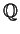 ).
).