Algebra Prelim, August 2010

Do all problems

1. Let G be a group of order 105 with a normal Sylow 3-subgroup. Show that G is abelian.

2. Find the Galois group of f (x) = x⁴ -2x² - 2 over Q, describing its generators explicitly as permutations of the roots of f.

3. Let p be a prime. Prove that the extension F_pⁿ⊃F_p has Galois group generated by the Frobenius automorphism σ : F_pⁿ -> F_pⁿ given by σ(a) = a^p for all a∈F_pⁿ.

4. Show that there is no 3 by 3 matrix A with entries in Q, such that A⁸ = I but A⁴≠I.

5. Let R be an integral domain. A nonzero nonunit element p∈R is prime if p | ab implies p | a or p | b. A nonzero nonunit element p∈R is irreducible if p = ab implies a or b is a unit. Show that

   (a)

   Every prime is irreducible.

   (b)

   If R is a UFD, then every irreducible is prime.

6. Let R be the ring Z/6Z and let I be the ideal 3Z/6Z. Prove that I⊗_RI≌I as R-modules.

7. Let S be a multiplicatively closed nonempty subset of the commutative ring R with a 1. Assume that 0 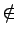$\notin$S.

   (a)

   Show that if R is a PID, then S^-1R is a PID.

   (b)

   Show that if R is a UFD, then S^-1R is a UFD.

8. Let R be a commutative ring with a 1.

   (a)

   Show that if x∈R is nilpotent and y∈R is a unit in R, then x + y is a unit in R.

   (b)

   Let f = a₀ + a₁x + a₂x² + ... + a_nxⁿ∈R[x]. Show that f is a unit in R[x] if an only if a₀ is a unit in R and a_i is nilpotent for i > 0.