Algebra Prelim Solutions, Fall 2007
- Let G be a simple group of order 168.
The number of Sylow 7-subgroups of G is congruent to 1 mod 7 and
divides
168/7 = 24. This number cannot be 1 because that would
mean that G has exactly one Sylow 7-subgroup, consequently G
would have a normal Sylow 7-subgroup and we would deduce that G is
not simple, contrary to the hypothesis. It follows that G has
exactly 8 Sylow 7-subgroups. Also by Lagrange's theorem, two
distinct Sylow 7-subgroups must intersect in the identity. Since any
element of order 7 is contained in a Sylow 7-subgroup and there are 6
elements of order 7 in each Sylow 7-subgroup, we deduce that there
are 8*6 = 48 elements of order 7 in G.
- Note that
ρ = i. The following are easy to check:
Q(√2)≠Q√3. Thus
Q(√2,√3) is a Galois extension of degree 4
over
Q.
Let K be the splitting field of x4 - 2 over
Q and let
L be the splitting field of x2 - 3 over
Q.
The roots of x4 - 2 are
± 4√2,
±i 4√2, hence
K is a Galois extension of degree 8 over
Q, and has
maximal real subfield of degree 4 over
Q, namely
Q( 4√2). Since this subfield is not normal over
Q, we deduce that
Q(√2,√3) is not
contained in K. Therefore
K∩L = Q, and we deduce
that
K∩L(i) = Q(i). The Galois
group of
L/Q has order two and is therefore isomorphic
Z/2Z. Also the Galois group of
K/Q is
a group of order 8 and not every subgroup is normal, because
Q(4√2) is not normal over
Q. and we
deduce that this group is isomorphic to the dihedral group D8 of
order 8. Finally
Gal(K/Q(i))≌Z/4Z, being generated by the automorphism
determined by
4√2 | --> i 4√2.
- (a)
- The Galois group of
(x4 -2)(x2 - 3) over
Q is
Gal(K/Q)×Gal(L/Q)≌D8×Z/2Z. The Galois group of
(x4 -2)(x2 - 3)
over
Q(i) is
Gal(K/Q(i))×Gal(L(i)/Q(i))≌Z/4Z×Z/2Z.
- (b)
-
Q(i) is Galois over
Q because it is the
splitting field of x2 + 1 over
Q.
- (c)
- Yes, because
Gal(LK/Q(i)) has nontrivial normal
subgroups.
- Since
0 --> A -- f--> B -- g--> C --> 0 is split
exact, there exists
h : B --> A such that hf = 1A, the
identity map on A. Then
(1D
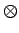 h)(1D
h)(1D 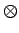 f )= 1D
f )= 1D 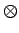 hf = 1D
hf = 1D 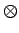 1A = 1. Thus if
x∈D
1A = 1. Thus if
x∈D 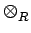 A and
(1D
A and
(1D 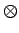 f )(x) = 0, then
(1D
f )(x) = 0, then
(1D 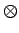 f )(1D
f )(1D 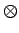 h)(x) = 0, consequently 1(x) = 0 and we conclude that x = 0, as required.
h)(x) = 0, consequently 1(x) = 0 and we conclude that x = 0, as required.
- Certainly S-1R is an integral domain, since it is a subring of
the field of fractions of R, so we need to prove that every ideal
of S-1R is principal.
Let
I <| S-1R and let
J = I∩R. Then
J <| R,
so J = xR for some
x∈R. Obviously
xS-1R⊆I, so
it remains to prove that
xS-1R⊇I. However if
y∈I, then
sy∈I∩R = J where
s∈S and hence we may
write sy = xr for some
r∈R. Therefore
y = s-1(sy) = xs-1r∈xS-1R and the result is proven.
- Let G be a group of order
24·112. The number of Sylow
11-subgroups is congruent to 1 mod 11 and divides 16, consequently
there is exactly one Sylow 11-subgroup; call this Sylow 11-subgroup
H. Then
H <| G. Now G/H and H are p-groups for p = 2
and 11 respectively, and p-groups are solvable (even nilpotent).
However the property of being solvable is closed under extensions,
that is H and G/H solvable implies G is solvable, which is the
required result.
- (a)
- Apply Eisenstein's criterion for the prime 3.
- (b)
- We know that f is irreducible (from (a)) and that g is
irreducible (use Eisenstein for the prime 2). Since
Q[x]
is a PID, we see that (f ) and (g) are maximal ideals of
Q[x]. Furthermore
(f )≠(g), because f and g are
not scalar multiples of each other. It now follows from the Chinese
remainder theorem that
Q[x]/(fg)≌Q[x]/(f )×Q[x]/(g), a product of two fields. The dimension
over
Q of these two fields are the degrees of the
polynomials f and g, that is 4 and 2 respectively.
- (a)
- Since
1·0 = 0, we see that
0∈t(X). Next suppose that
x, y∈t(X). Then there exist
r, s∈R\ 0 such that
rx = 0 = sy and we have
(rs)(x + y) = 0. Since
rs≠ 0 because
R is an integral domain, we conclude that
x + y∈t(X). Finally
suppose that
x∈t(X) and
r∈R. Then there exists
s∈R\ 0 such that sx = 0 and consequently s(rx) = 0. This
shows that
rx∈t(X) and we have established that t(X) is an
R-submodule of X.
- (b)
- Write T = t(X) and let
x∈t(T); we want to prove that
x∈T. Since
x∈t(T), there exists
s∈R\ 0 such that
sx∈T, and then there exists
t∈R\ 0 such that
t(sx) = 0. It follows that (st)x = 0 and since
st≠ 0
because R is an integral domain, we conclude that
x∈T as
required.
- (c)
- Because t(X/t(X)) is cyclic,
t(X/t(X))≌R/I for some
I <| R. But
t(X/t(X)) = 0 by (b), hence I = 0 and we
deduce that
X/t(X)≌R. Since R
is a projective R-module,
0 --> t(X) --> X --> X/t(X) --> 0 splits, in particular
X≌t(X)⊕R, as required.
Peter Linnell
2007-08-11