Algebra Prelim, August 2007
Do all problems
- How many elements of order 7 must there be in a simple group of order
168?
- Let
ρ be a primitive 4th root of 1 over
Q.
- (a)
- Compute the Galois group of
(x4 -2)(x2 - 3) over
Q and
Q(ρ).
- (b)
- Is
Q(ρ) Galois over
Q? (Explain your
answer.)
- (c)
- Are there any proper subfields of the splitting field of
(x4 -2)(x2 - 3) over
Q(ρ) that are Galois over
Q(ρ)? (Explain your answer.)
- Suppose that
0 --> A -- f--> B -- g--> C --> 0 is
a split exact sequence of left R-modules, where R is a ring with
a 1. If D is a right R-module, prove that
1
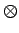 f : D
f : D 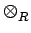 A --> D
A --> D 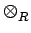 B is a monomorphism.
B is a monomorphism.
- Let R be a PID and let S be a multiplicatively closed subset of
R. Assume that S is nonempty and that S does not contain 0.
Prove that S-1R is a PID.
- Prove that a group of order
24·112 is solvable.
- Prove that
f (x) = x4 + 9x - 30 is an irreducible polynomial over
Q.
- Let
g(x) = x2 + 2 and let I be the ideal in
Q[x]
generated by the product f (x)g(x). Show that
Q[x]/I is
the product of two fields. What is the dimension over
Q
of these fields?
- Let R be an integral domain. If X is an R-module, then let
t(X) denote the subset
{x∈X | rx = 0 for some nonzero
r∈R}.
- Prove that t(X) is a submodule of X.
- Prove that
t(X/t(X)) = 0.
- Prove that if X/t(X) is a nonzero cyclic R-module, then X is
isomorphic to
t(X)⊕R.
Peter Linnell
2007-08-11