Algebra Prelim, Fall 2005
Do all problems
- Show that there are exactly 5 nonisomorphic groups of order 18.
- Let A be a commutative ring and set
B = A[X, Y]/(X2 - Y2). Prove
that A is a Noetherian ring if and only if B is a Noetherian
ring.
- Let F be a field with more than 2 elements and let
GL2(F)
denote the group of
2 X 2 invertible matrices with entries in
F. Consider the action of
GL2(F) on one-dimensional subspaces
of F2. Show that the stabilizer of a one-dimensional subspace is
never simple.
- Let R be the ring
Z[X] and set
M = 2R + XR. Prove or
disprove: M is a free R-module.
- Let F be a field of characteristic zero. Suppose that K/F is
finite Galois extension with Galois group G. Prove that if
a e K and
s(a) - a e F for all
s e G, then
a e F.
- Let S be a simple algebra of finite dimension n over
C. Prove that there are
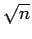 maximal left ideals of
S whose intersection is zero.
maximal left ideals of
S whose intersection is zero.
- Recall that if F is a field, then the tensor product of two
F-algebras (over F) is another F-algebra. Let L be a finite
field extension of F and let
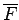 be the algebraic
closure of F. Show that if
be the algebraic
closure of F. Show that if
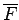
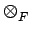 L is a field,
then F = L.
L is a field,
then F = L.
Peter Linnell
2005-08-20