Algebra Prelim, Fall 2004
Do all problems
- An automorphism of a group is an isomorphism of the group with
itself. The set of automorphisms
Aut(G) of a group G
is itself a group under composition of functions.
Find the group of automorphisms of the cyclic group C2p of
order 2p where p is an odd prime.
- Let G be a simple group of order
4032 = 8!/10.
Prove that G is not isomorphic to a subgroup of the alternating
group A8. Deduce that G has at least 216 elements of order 7.
- An ideal I in a commutative ring R with unit is called
primary if
I =/= R and whenever
ab e I and
a
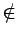 I, then
bn e I for some positive integer n.
Prove that if R is a PID, then I is primary if and only if I = Pn for some prime ideal P of R and some positive integer
n.
I, then
bn e I for some positive integer n.
Prove that if R is a PID, then I is primary if and only if I = Pn for some prime ideal P of R and some positive integer
n.
- Let k be a field and let
k[x2, x3] denote the subring of the
polynomial ring k[x] generated by k
and
{x2, x3}. Prove that every
ideal of R can be generated by two elements. Hint: if the ideal is
nonzero, we may choose one of the generators to be a polynomial of
least degree.
- Let k be a field, let
f e k[x] be a polynomial of positive
degree and let M be a finitely generated k[x]-module.
Suppose every element of M can be written in the form fm where
m e M. Prove that M has finite dimension as a vector space
over k.
- Let R be an integral domain (commutative ring with
1 =/= 0 and
without nontrivial zero divisors)
and suppose R when viewed as a left
R-module is injective. Prove that R is a field.
- Let K be a splitting field over the rational numbers
Q
of the polynomial x4 + 16. Determine the Galois group of
K/Q.
Peter Linnell
2004-08-25