We now count elements. The number of elements of order 47 is 46*48; the number of elements of order 3 is at least 2*16, and the number of elements of order a power of two is at least 17. We now have at least 17 + 2*16 + 46*48 = 2257 elements in G, which is too many. This proves that there is no simple group of order 2256.
- (i)
- Every element of G can be written in the form
xa1yb1...xanybn, where
ai, bi
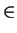 Z. Using
x7 = y3 = 1, we may assume that
ai, bi> 0 for all i. Now whenever
there is a subword yx, we can replace it with xy2, because
yxy-1 = x2, so we may push all the x's to the left and all
the y's to the right. This proves the result.
Z. Using
x7 = y3 = 1, we may assume that
ai, bi> 0 for all i. Now whenever
there is a subword yx, we can replace it with xy2, because
yxy-1 = x2, so we may push all the x's to the left and all
the y's to the right. This proves the result.
- (ii)
- Using (i) and
x7 = y3 = 1, we may write every element of G in
the form xiyj where
0 < i < 6 and
0 < j < 2. It
follows that
| G| < 7*3 = 21.
- (iii)
- This is because
q respects the relations. Specifically,
(1 3 4 5 6 7)7 = 1,
((2 3 5)(4 7 6))3 = 1,
((2 3 5)(4 7 6))(1 2 3 4 5 6 7)((2 3 5)(4 7 6))-1 = (1 3 5 7 2 4 6).
- (iv)
- We see from (iii) that imq has elements of order 7 and 3. Therefore 21 divides | imq| and hence 21 divides | G|. Since | G| < 21 from (ii), we deduce that | G| = 21 as required.
We now apply the structure theorem for finitely generated modules over a PID. We may write
| M | @ Ra |
|
| N | @ Rb |
where n, a, b, ai, bi are non-negative integers and the qi are nonassociate prime powers. Since M
R2a 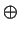 (R/q1R)2a1
(R/q1R)2a1 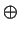 ...
... 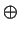 (R/qnR)2an @ R2b
(R/qnR)2an @ R2b 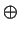 (R/q1R)2b1
(R/q1R)2b1 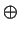 ...
... 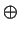 (R/qnR)2bn.
(R/qnR)2bn.
By the uniqueness part of the structure theorem, we deduce that
2a = 2b,
2a1 = 2b1, ...,
2an = 2bn. Therefore
a = b, a1 = b1, ..., an = bn and the result follows.
- (i)
- Note that f has degree 4. Since
ai satisfies f, we
have
[K(ai) : K] < 4. Therefore
[K(ai,aj) : K] < 4*4 = 16, in particular
K(ai,aj) =/= L as
required.
- (ii)
- Assume that f is monic. Then if a
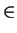 K is the coefficient of
x3 of f, we have
a1 + a2 + a3 + a4 = - a.
Since L is the splitting field over K of the polynomial f and
we are in characteristic zero, L is a Galois extension of K. Let
G denote the Galois group of L over K. Then the subfields of
L containing K are in a one-to-one correspondence with the
subgroups of G, and G permutes the
ai faithfully. If
K(a1 + 2a2 + 3a3) =/= L, then
K(a1 + 2a2 + 3a3) corresponds to a nontrivial
subgroup of G, in particular
a1 + 2a2 + 3a3 is
fixed by some nontrivial permutation of the
ai. In other
words there is
1 =/= s
K is the coefficient of
x3 of f, we have
a1 + a2 + a3 + a4 = - a.
Since L is the splitting field over K of the polynomial f and
we are in characteristic zero, L is a Galois extension of K. Let
G denote the Galois group of L over K. Then the subfields of
L containing K are in a one-to-one correspondence with the
subgroups of G, and G permutes the
ai faithfully. If
K(a1 + 2a2 + 3a3) =/= L, then
K(a1 + 2a2 + 3a3) corresponds to a nontrivial
subgroup of G, in particular
a1 + 2a2 + 3a3 is
fixed by some nontrivial permutation of the
ai. In other
words there is
1 =/= s 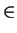 S4 such that
a1 + 2a2 + 3a3 = as1 + 2as2 + 3as3.By inspection, this will yield a different linear relation from a1 + a2 + a3 + a4 = - a from above. (Clearly this relation is not 0 = 0. If we subtract the right hand side from the left hand side, then the sum of the coefficients of the ai is 0.) Therefore we may express the ai in terms of just two of the ai; in other words, L = K(ai,aj) for some i, j, which contradicts (i). Finally K[a1 + 2a2 + 3a3] = K(a1 + 2a2 + 3a3) because a1 + 2a2 + 3a3 is algebraic over K and the result follows.
S4 such that
a1 + 2a2 + 3a3 = as1 + 2as2 + 3as3.By inspection, this will yield a different linear relation from a1 + a2 + a3 + a4 = - a from above. (Clearly this relation is not 0 = 0. If we subtract the right hand side from the left hand side, then the sum of the coefficients of the ai is 0.) Therefore we may express the ai in terms of just two of the ai; in other words, L = K(ai,aj) for some i, j, which contradicts (i). Finally K[a1 + 2a2 + 3a3] = K(a1 + 2a2 + 3a3) because a1 + 2a2 + 3a3 is algebraic over K and the result follows.