Algebra Prelim, Fall 2003
Do all problems
- Prove that a group of order
2256 = 47*48 cannot be simple.
- Let
G = < x, y | x7 = y3 = 1, yxy-1 = x2 >.
- (i)
- Prove that every element of G can be written in the form xiyj
where i, j are non-negative integers.
- (ii)
- Prove that G has order at most 21.
- (iii)
- Prove that there is a homomorphism
q : G - > S7 such
that
qx = (1 2 3 4 5 6 7), qy = (2 3 5)(4 7 6).
- (iv)
- Prove that G has order 21.
- Let R be a UFD. Suppose that for every coprime p, q
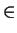 R, the
ideal pR + qR is principal. Prove that for every a, b
R, the
ideal pR + qR is principal. Prove that for every a, b 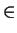 R, the
ideal aR + bR is principal.
(Coprime means that the greatest common divisor of p, q is 1.)
R, the
ideal aR + bR is principal.
(Coprime means that the greatest common divisor of p, q is 1.)
- Let R be the ring
Z/4Z and let M be the
ideal
2Z/4Z. Prove that
M
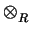 M @ M as R-modules.
M @ M as R-modules.
- Let R be a PID and let M, N be R-modules. Suppose M is
finitely generated and
M
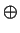 M @ N
M @ N 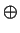 N. Prove that
M @ N.
N. Prove that
M @ N.
- Let K be a field of characteristic zero, let
f
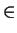 K[x] be an
irreducible polynomial, let L be a splitting field for f over
K, and let
a1,a2,a3,a4
K[x] be an
irreducible polynomial, let L be a splitting field for f over
K, and let
a1,a2,a3,a4 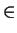 L be the
roots of f. Suppose
[L : K] = 24 (i.e.
dimKL = 24).
L be the
roots of f. Suppose
[L : K] = 24 (i.e.
dimKL = 24).
- (i)
- If
1 < i, j < 4 are integers, prove
that
L =/= K(ai,aj).
- (ii)
- Prove that
L = K[a1 + 2a2 + 3a3].
- Let k be an algebraically closed field, let n be a positive
integer, and let U, V be affine algebraic sets in kn (so
U is the zero set of a collection of polynomials in
k[x1,..., xn]). Suppose
U /\ V = f.
Prove that
I(U) + I(V) = k[x1,..., xn]
(where
I(U) is the set of all polynomials in
k[x1,..., xn] which vanish on U).
Peter Linnell
2003-08-04