- (a)
- H acts on the set of conjugates of Q according to the formula
gQg-1 | - > hgQg-1h-1 for h
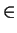 H and g
H and g 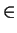 G.
Note that
gQg-1 < G for all g, so
OQ is a set of
subgroups. Let
S = {h
G.
Note that
gQg-1 < G for all g, so
OQ is a set of
subgroups. Let
S = {h 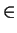 H | hQh-1 = Q},
the stabilizer of Q in H. Then
|OQ|| S| = | H|.
Now h
H | hQh-1 = Q},
the stabilizer of Q in H. Then
|OQ|| S| = | H|.
Now h 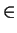 S if and only if
h
S if and only if
h 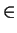 H /\ NG(Q) = 1,
hence | S| = 1 and the result follows.
H /\ NG(Q) = 1,
hence | S| = 1 and the result follows.
- (b)
- Let P be a Sylow p-subgroup of G. We apply the above with H = P. Since P /\ NG(Q) = P /\ Q = 1, we see that OQ has | P| = pm subgroups. Furthermore all the subgroups of OQ have prime order q, so any two of them must intersect in 1. Now each nonidentity element of a subgroup in OQ has order q, consequently each subgroup of OQ yields q - 1 elements of order q and we deduce that G has at least (q - 1)pm elements of order q. Therefore G has at most pqm - (q - 1)pm = pm elements of order a power of p. Since | P| = pm and every element of a Sylow p-subgroup has order a power of p, we conclude that P is the only Sylow p-subgroup of G. Therefore P is normal in G and we are finished.
Next we show that
![]()
![]() Q(
Q(![]() ). Suppose
). Suppose
![]()
![]() Q(
Q(![]() ). Then we could write
). Then we could write
![]() = a + b
= a + b![]() with
a, b
with
a, b ![]() Q,
because every element of
Q(
Q,
because every element of
Q(![]() ) can
be written in this form. Squaring, we obtain
3 = a2 + 2b2 + 2ab
) can
be written in this form. Squaring, we obtain
3 = a2 + 2b2 + 2ab![]() . Since
. Since
![]()
![]() Q, we deduce that a
or b = 0. But a = 0 yields
Q, we deduce that a
or b = 0. But a = 0 yields
![]()
![]() Q, while
b = 0 yields
Q, while
b = 0 yields
![]()
![]() Q, neither of which is true.
We conclude that
Q, neither of which is true.
We conclude that
![]()
![]() Q(
Q(![]() ). Since
). Since
![]() satisfies x2 - 3, we deduce that
[F : Q(
satisfies x2 - 3, we deduce that
[F : Q(![]() )] = 2. Therefore
)] = 2. Therefore
Suppose
![]()
![]() K. Since
K. Since
![]() satisfies x8 - 2
and x8 - 2 is irreducible over
Q by Eisenstein's
criterion for the prime 2, we see that 8 divides
[K : Q],
consequently 8 divides
| Gal(K/Q)|. But
| Gal(K/Q)| = 4| N|, so this is not possible if | N| is odd.
satisfies x8 - 2
and x8 - 2 is irreducible over
Q by Eisenstein's
criterion for the prime 2, we see that 8 divides
[K : Q],
consequently 8 divides
| Gal(K/Q)|. But
| Gal(K/Q)| = 4| N|, so this is not possible if | N| is odd.
- (a)
- If X and Y are right R-modules and
q : X - > Y is
an R-module homomorphism, then there is a unique group homomorphism
q
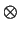 1 : X
1 : X 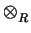 C - > Y
C - > Y 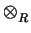 C such that
q(x
C such that
q(x 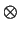 c) = (qx)
c) = (qx) 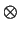 c for all x
c for all x 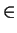 X and
c
X and
c 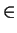 C.
C.
First we apply this to the maps
(a, b) | - > a : A 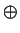 B - - > A
B - - > A(a, b) | - > b : A 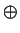 B - - > B.
B - - > B.
We obtain a group homomorphismq : (Asuch that q((a, b)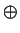 B)
B) 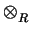 C - - > A
C - - > A 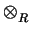 C
C 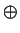 B
B 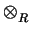 C
C
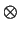 c) = (a
c) = (a 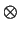 c, b
c, b 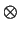 c).
Next we apply it to the maps
c).
Next we apply it to the maps
a | - > (a, 0) 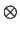 c : A
c : A 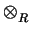 C - - > (A
C - - > (A 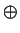 B)
B) 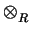 C
Ca | - > (0, b) 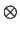 c : B
c : B 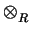 C - - > (A
C - - > (A 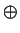 B)
B) 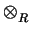 C.
C.
We obtain a group homomorphismf : (Asuch that f(a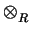 C)
C) 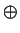 (B
(B 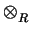 C) - - > (A
C) - - > (A 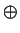 B)
B) 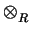 C
C
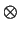 c, b
c, b  d )= (a, 0)
d )= (a, 0)  c + (0, b)
c + (0, b)  d.
d.
Finally we show that fq is the identity on (A
 B)
B) 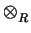 C, and that
qf is the identity on
(A
C, and that
qf is the identity on
(A 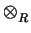 C)
C) 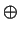 (B
(B 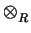 C). We have
fq(a, b)Since (A
C). We have
fq(a, b)Since (A c = f(a
c = f(a  c, b
c, b  c) = (a, b)
c) = (a, b)  c.
c.
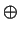 B)
B) 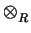 C is generated as an abelian group by
elements of the form
(a, b)
C is generated as an abelian group by
elements of the form
(a, b) 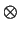 c, we see that
fq is
the identity. Also
qf(aSince (A
c, we see that
fq is
the identity. Also
qf(aSince (A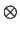 c, b
c, b 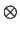 d )= q(a, 0)
d )= q(a, 0) 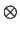 c + q(0, b)
c + q(0, b) 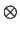 d = (a
d = (a 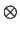 c, b
c, b  d ).
d ).
 C)
C)  (B
(B  C) is generated as an abelian
group by elements of the form
(a
C) is generated as an abelian
group by elements of the form
(a 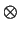 c, b
c, b 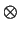 d ), we deduce
that
qf is the identity. It now follows that
(A
d ), we deduce
that
qf is the identity. It now follows that
(A 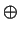 B)
B) 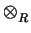 C @ (A
C @ (A 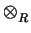 C)
C) 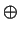 (B
(B 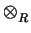 C).
C).
- (b)
- Since M is a finitely generated
Z-module, we may
express it as a finite direct sum of cyclic
Z-modules,
say
M =
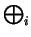 Z/aiZ, where we may
assume that
ai =/= ±1 for all i.
Then by the first part, we see that
MTherefore it will be sufficient to prove Z/aiZ
Z/aiZ, where we may
assume that
ai =/= ±1 for all i.
Then by the first part, we see that
MTherefore it will be sufficient to prove Z/aiZ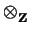 M @
M @  Z/aiZ
Z/aiZ 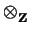 Z/ajZ.
Z/ajZ.
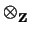 Z/aiZ =/= 0 for all i
(of course even for just one i will be sufficient). However we can
define a bilinear map
q : Z/aiZ X Z/aiZ - > Z/aiZby q(x, y) = xy. This induces a Z-module homomorphism Z/aiZ
Z/aiZ =/= 0 for all i
(of course even for just one i will be sufficient). However we can
define a bilinear map
q : Z/aiZ X Z/aiZ - > Z/aiZby q(x, y) = xy. This induces a Z-module homomorphism Z/aiZ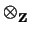 Z/aiZ - > Z/aiZ, which is
obviously onto. We conclude that
Z/aiZ
Z/aiZ - > Z/aiZ, which is
obviously onto. We conclude that
Z/aiZ 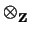 Z/aiZ =/= 0, as required.
Z/aiZ =/= 0, as required.
Conversely suppose every R-module is projective. Since R is an integral domain, to prove R is a field we only need show that every nonzero element of R is invertible. Suppose to the contrary that x is a nonzero element of R which is not invertible. Then R/Rx is a nonzero R-module, so it has a nonzero element u. Note that xu = 0. Consider the exact sequence
Now suppose L is a normal subgroup of G such that Z(G/L) = 1 and L does not contain ZN. Then there is a nonnegative integer n such that
| ( |
|
) |
with
a, b ![]() Q. Note that if
f
Q. Note that if
f ![]() Q[x],
then (x - 1) divides
f (x) - f (1), consequently
f (x)(x + 1) + (x2 - 1) = f (1)(x + 1) + (x2 - 1) in
Q[x]/(x2 - 1).
Q[x],
then (x - 1) divides
f (x) - f (1), consequently
f (x)(x + 1) + (x2 - 1) = f (1)(x + 1) + (x2 - 1) in
Q[x]/(x2 - 1).
Now we verify that I is a left ideal of Q[x]/(x2 - 1). Clearly I is an abelian group under addition. Since
| ( |
|
) | ( |
|
) | = | ( |
|
) |
we see that I is closed under left multiplication by elements of Q[x]/(x2 - 1), and it now follows that I is a left ideal.
Finally we need to show that I is a minimal ideal. Obviously
I =/= 0 (note
x + 1![]() (x2 - 1)). Suppose J is a nonzero left
ideal contained in I. We need to show that J = I.
By multiplying on the left by the matrix
(x2 - 1)). Suppose J is a nonzero left
ideal contained in I. We need to show that J = I.
By multiplying on the left by the matrix
| ( |
|
) |
if necessary, we may assume that I contains a matrix of the form
| ( |
|
) |
with a =/= 0. Then by multiplying on the left by
| ( |
|
) |
we see that J must be the whole of I and the result follows.