Algebra Prelim, Summer 2002
Instructions: do all problems.
- Let G be a finite group.
- (a)
- Let H and Q be subgroups of G. Note that H
acts on the set of conjugates of Q via conjugation. Let
OQ denote the orbit containing Q with respect to this
action. Prove that if
H /\ NG(Q) = 1, then the orbit
OQ has | H| subgroups in it.
- (b)
- Now suppose that
| G| = pmq where p and q are distinct primes
and m is a positive integer. Let Q be a Sylow q-subgroup of
G and suppose that
NG(Q) = Q. Prove that G has a normal
Sylow p-subgroup.
- Let K be a finite Galois extension of the rationals
Q.
Suppose that
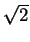 and
and 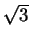 are both elements of K.
Show that
Gal(K/Q) has a normal subgroup N of index
4. Show further that if | N| is odd, then
are both elements of K.
Show that
Gal(K/Q) has a normal subgroup N of index
4. Show further that if | N| is odd, then
![$ \sqrt[8]{2}$](img3.gif)
 K.
K.
- (a)
- Let R be a ring. Let A and B be right R-modules and let C
be a left R-module. Prove that
(A
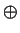 B)
B) 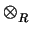 C @ (A
C @ (A 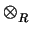 C)
C) 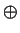 (B
(B 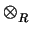 C).
C).
- (b)
- Let M be a finitely generated
Z-module. Prove that if
M
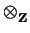 M = 0, then M = 0.
M = 0, then M = 0.
- Let R be a commutative Noetherian ring with unity and let M be a
nonzero R-module. Given m
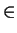 M, set
Ann(m) = {r
M, set
Ann(m) = {r 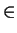 R | rm = 0}. Show there exists some w
R | rm = 0}. Show there exists some w 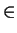 M such that
Ann(w) is
a prime ideal of R.
M such that
Ann(w) is
a prime ideal of R.
- Let R be an integral domain. Prove that R is a field if and only
if every R-module is projective.
- Denote the center of a group by
Z(·). Let G be a
finite group with identity element e. Define a sequence of
subgroups of G inductively by
Z0 = {e} and
Zj + 1 is the preimage in G of Z(G/Zj).
Since
Z0 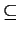 Z1
Z1 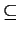 Z2
Z2 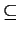 ..., there is a positive integer
N such that
ZN = ZN + 1 = ZN + 2.... Prove that
ZN is equal to the intersection of all normal subgroups K
in G such that
Z(G/K) is the trivial group.
..., there is a positive integer
N such that
ZN = ZN + 1 = ZN + 2.... Prove that
ZN is equal to the intersection of all normal subgroups K
in G such that
Z(G/K) is the trivial group.
- Explicitly find a simple (i.e. minimal) left ideal of the following
ring of
2 X 2 matrices:
M2(Q[x]/(x2 - 1)).
Peter Linnell
2002-08-17
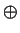 B)
B) 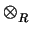 C @ (A
C @ (A 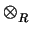 C)
C) 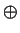 (B
(B 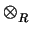 C).
C).
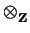 M = 0, then M = 0.
M = 0, then M = 0.