Algebra Qualifying Exam, Summer 2001
Instructions: do all problems.
- Let G be a group.
- (a)
- Show that if A and B are normal subgroups of G, then A
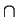 B
is also a normal subgroup of G.
B
is also a normal subgroup of G.
- (b)
- Suppose that N is a proper nontrivial normal simple subgroup of
G and that G/N is also a simple group. Prove that either N is
the only nontrivial proper normal subgroup of G or that G is
isomorphic to
N X G/N.
- Let A be a finite noncyclic abelian group with two generators. Let
p be a prime. Assume that for all primes q with q
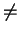 p, there
are no nonzero group homomorphisms from
Z/(q) to A.
Describe the structure of A and prove that there is no nonzero
group homomorphism from A to
Z/(q) for all primes q
with q
p, there
are no nonzero group homomorphisms from
Z/(q) to A.
Describe the structure of A and prove that there is no nonzero
group homomorphism from A to
Z/(q) for all primes q
with q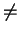 p.
p.
- Let R be a ring with a 1
and let
0 - > P - > M - > Q - > 0 be a short
exact sequence of R-modules. Show that if P and Q are
projective R-modules, then M is a projective R-module.
- Prove that every group of order 441 has a quotient which is
isomorphic to
Z/(3).
- Let R be a commutative ring with a 1
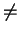 0.
Suppose that every ideal of
R different from R is a prime ideal.
0.
Suppose that every ideal of
R different from R is a prime ideal.
- (a)
- Prove that R is an integral domain.
- (b)
- Prove that R is a field.
- (a)
- Prove that
Q(
![$ \sqrt[4]{2}$](img3.gif) ) and
Q(i
) and
Q(i![$ \sqrt[4]{2}$](img3.gif) )
are isomorphic fields.
)
are isomorphic fields.
- (b)
- Prove that
Q(i,
![$ \sqrt[4]{2}$](img3.gif) ) is a Galois extension of
Q.
) is a Galois extension of
Q.
- (c)
- Find the Galois group
Gal(Q(i,
![$ \sqrt[4]{2}$](img3.gif) )/Q)
and prove your claim.
)/Q)
and prove your claim.
- Recall that a group G of permutations of a set S is called
transitive if given s, t
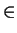 S, then there exists
s
S, then there exists
s 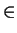 G such that
s(s) = t. Let K be a field. Let f (x) be a
separable polynomial in K[x] and let F be a splitting field of
f over K. Prove that f (x) is irreducible over K if and only
if the Galois group of F over K is a transitive group when viewed
as a group of permutations of the roots of f (x).
G such that
s(s) = t. Let K be a field. Let f (x) be a
separable polynomial in K[x] and let F be a splitting field of
f over K. Prove that f (x) is irreducible over K if and only
if the Galois group of F over K is a transitive group when viewed
as a group of permutations of the roots of f (x).
- An ideal in a commutative ring R with a 1 is called primary
if I
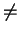 R and if ab
R and if ab 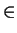 I and
a
I and
a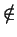 I, then bn
I, then bn 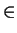 I for
some positive integer n.
I for
some positive integer n.
- (a)
- Prove that prime ideals are primary.
- (b)
- Prove that if R is a PID, then I is primary if and only if
I = Pn for some prime ideal P of R.
Peter Linnell
2001-09-01
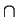 B
is also a normal subgroup of G.
B
is also a normal subgroup of G.
![$ \sqrt[4]{2}$](img3.gif) ) and
Q(i
) and
Q(i![$ \sqrt[4]{2}$](img3.gif) )
are isomorphic fields.
)
are isomorphic fields.
![$ \sqrt[4]{2}$](img3.gif) ) is a Galois extension of
Q.
) is a Galois extension of
Q.
![$ \sqrt[4]{2}$](img3.gif) )/Q)
and prove your claim.
)/Q)
and prove your claim.