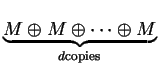ALGEBRA PRELIMINARY EXAMINATION:
Fall 2000
Do all problems
- Let
1 - - > A - - > G - - > P - - > 1
be a short exact sequence of groups such that A is abelian,
| P| = 81, and | A| = 332. Show that G has a nontrivial center.
- Let F be a finite field of odd characteristic. Prove that the rings
F[X]/(X2 - a)
as
a ranges over all nonzero elements of F fall into exactly
two isomorphism classes.
- Let R be a finite-dimensional simple algebra and let M be a
finite-dimensional left R-module. Prove that there is a positive
integer d such that
is a free module.
- Let B be a square matrix with rational entries. Show that if there
is a monic polynomial
f
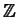 [T] such that f (B) = 0
then the trace of B is an integer.
[T] such that f (B) = 0
then the trace of B is an integer.
- Let k be a field. Compute the dimension over k of
k[
X]/(
Xm)
![$\displaystyle \otimes_{k[X]}^{}$](img4.gif) k
k[
X]/(
Xn)
and prove your assertion.
- In this problem X, Y, Z are indeterminates. Define
s :
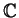 (X, Y, Z) - >
(X, Y, Z) - > 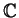 (X, Y, Z) by
s(h(X, Y, Z)) = h(Y, Z, X)
for every rational function h in three variables. Prove or disprove:
every member of
(X, Y, Z) by
s(h(X, Y, Z)) = h(Y, Z, X)
for every rational function h in three variables. Prove or disprove:
every member of
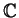 (X, Y, Z) which is left unchanged
by
s is a rational function of
X + Y + Z, XY + YZ + XZ and XYZ.
(X, Y, Z) which is left unchanged
by
s is a rational function of
X + Y + Z, XY + YZ + XZ and XYZ.
Peter Linnell
2000-08-27
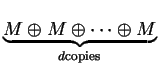
![$\displaystyle \otimes_{k[X]}^{}$](img4.gif) k[X]/(Xn)
k[X]/(Xn)