2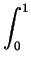
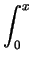 f (x + y) dydx =
f (x + y) dydx = 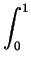
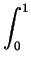 f (x + y) dydx.
f (x + y) dydx.
Also
af'(ax)f (bx) + bf (ax)f'(bx) = f'(x)
holds for all
x, and for all
a,b satisfying
a2 + b2 = 1. Hence
(a + b)f'(0) = f'(0) holds. By
taking
a = b = 1/
f (x) = (f (2-m/2x))2m.
Now fix any x, and
d > 0. There is a positive integer N
such that for all m
(1 + 2-m - 1(c - d)x2)2m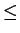 f (x)
f (x)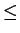 (1 + 2-m - 1(c + d)x2)2m.
(1 + 2-m - 1(c + d)x2)2m.
Now let
m - >
e(c - d)x2/2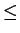 f (x)
f (x)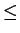 e(c + d)/x2.
e(c + d)/x2.
Since
d was arbitrary,
f (x) = ecx2/2. Using the
condition f (1) = 2, we conclude that
f (x) = 2x2.
en(d)/n < ln(M)(ln(1/d)).
The result follows.
3 X 4 + 3 X 4 + 3 X 5 + 3 X 5 + 4 X 5 + 4 X 5 = 94
plus the points at the corners, which form eight 1/8th spheres of radius 1, plus the points which form 12 1/4th cylinders whose heights are 3,4,5. It follows that the volume required is
60 - 6 + 94 + 4p/3 + 12p = 148 + 40p/3.
- (i)
- Obviously n > 4. Next, n
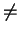 5 because 4 divides 3 + 5. Also n
5 because 4 divides 3 + 5. Also n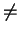 6 because 3 divides 6 and n
6 because 3 divides 6 and n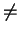 7 because 7
divides 3 + 4. Finally n
7 because 7
divides 3 + 4. Finally n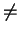 8 since 4 divides 8, and n
8 since 4 divides 8, and n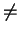 9
since 3 divides 9. On the other hand n = 10 because 3 does
not divide 4, 10 and 14. Furthermore 4 does not divide 3, 10 and 13,
and 10 does not divide 3, 4 and 7.
9
since 3 divides 9. On the other hand n = 10 because 3 does
not divide 4, 10 and 14. Furthermore 4 does not divide 3, 10 and 13,
and 10 does not divide 3, 4 and 7.
- (ii)
- Suppose {3, 4, 10, m} is contained in a set which has property ND. Then 3 should not divide m, so m is not of the form 3k. Also 3 should not divide 10 + m, so m is not of the form 3k + 2. Furthermore 33 should not divide m + 4 + 10, so m is not of the form 3k + 1. Here k denotes some integer. If s has property ND and contains 3,4 10 and m, then m cannot be of the form 3k, 3k + 1, 3k + 2. This is impossible and the statement is proven.