16th VTRMC, 1994, Solutions

1. Let I = ∫₀¹∫₀^x∫₀^1-x2e^(1-z)2 dzdydx. We change the order of integration, so we write I = ∫∫∫_Ve^(1-z)2 dV, where V is the region of integration.

   

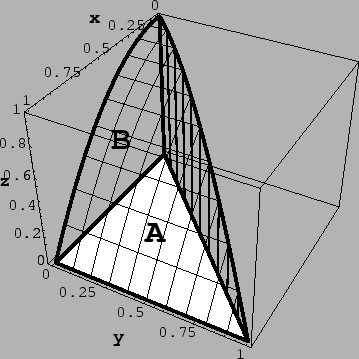
   It can be described as the cylinder with axis parallel to the z-axis and cross-section A, bounded below by z = 0 and bounded above by z = 1 - x². This region can also be described as the cylinder with axis parallel to the y-axis and cross-section B, bounded on the left by y = 0 and on the right by y = x. Therefore

   I = ∫₀¹∫₀^√1-z∫₀^xe^(1-z)2 dydxdz = ∫₀¹∫₀^√1-zxe^(1-z)2 dxdz = ∫₀¹(1 - z)e^(1-z)2/2 dz = [- e^(1-z)2/4]₀¹ = (e - 1)/4.

   
   

2. We need to prove that pq≤∫₀^pf (t) dt + ∫₀^qg(t) dt. Either q≤f (p) or q≥f (p) and without loss of generality we may assume that q≥f (p) (if q≤f (p), then we interchange x and y; alternatively just follow a similar argument to what is given below). Then we have the following diagram.

   
   
   

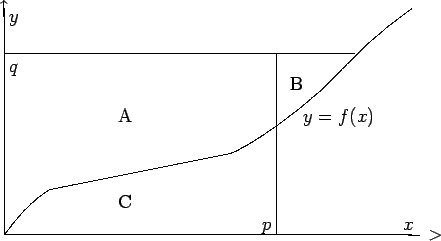
   We now interpret the quantities in terms of areas: pq is the area of A∪C, ∫₀^pf (t) dt is the area of C, and ∫₀^qg(t) dt is the area of A∪B. The result follows.

3. Differentiating both sides with respect to x, we obtain 2ff' = f² - f⁴ + (f')². Thus f⁴ = (f - f')², hence f - f' = ±f² and we deduce that dx/df = 1/(f±f²). We have two cases to consider; first we consider the + sign, that is dx/df = 1/f - 1/(f + 1) and we obtain x = ln| f| - ln| f + 1| + C, where C is an arbitrary constant. Now we have the initial condition f (0) = ±10. If f (0) = 10, we find that C = ln(11/10) and consequently x = ln(11/10) - ln|(f + 1)|/f|. Solving this for x, we see that f (x) = 10/(11e^-x - 10). On the other hand if f (0) = - 10, then C = ln(9/10), consequently x = ln(9/10) - ln|(f + 1)/f|. Solving this for x, we conclude that f (x) = 10/(9e^-x - 10).

   Now we consider the - sign, that is dx/df = 1/f - 1/(f - 1) and we obtain x = ln| f| - ln| f - 1| + D, where D is an arbitrary constant. If the initial condition f (0) = 10, we find that D = ln(9/10) and consequently x = ln| f /(f - 1)| + ln(9/10). Solving this for x, we deduce that f (x) = 10/(10 - 9e^-x). On the other hand if the initial condition is f (0) = - 10, then D = ln(11/10) and hence x = ln| f /(f - 1)| + ln(11/10). Solving for x, we conclude that f (x) = 10/(10 - 11e^-x).

   Summing up, we have

   f (x) = ±10/(10 - 9e^-x)     or     ±10/(10 - 11e^-x).

4. Set f (x) = ax⁴ + bx³ + x² + bx + a = 0. We will show that the maximum value of a + b is -1/2; certainly -1/2 can be obtained, e.g. with a = 1 and b = - 3/2, because in this case 1 is a root of f. Furthermore f (1) = 2(a + b) + 1, hence we may assume that 1 is not a root of f. Note that if α is a root of f, then so is 1/α. Thus we may assume that two of the roots of f are 1/α,α, where 1 < α is a real number.

   We claim that the other two roots of f cannot be positive. Indeed suppose β is another positive root of f, which we may suppose is not 1 (though could be α or 1/α). Since the product of the roots of f is a/a = 1, we see that the fourth root of f is 1/β. It now follows that the sum of the products of roots of f two at a time is greater than α(1/α) + β(1/β) = 2; however this sum is also 1/a and we have contradicted the hypothesis a > 1/2.

   Thus f has exactly two positive roots, namely 1/α,α, and by considering the graph of f, we see that f (1) < 0. Thus a + b + 1 + b + a < 0 and the result follows.

6. We follow the hint given, so suppose β is another eigenvector corresponding to 1 with components β_i ( 1≤i≤n). Choose t such that α_t/|β_t|≤α_i/|β_i| for all i (if β_i = 0, then we interpret α_i/|β_i| = + ∞; note that β_t≠ 0). Multiplying β by α_t/β_t, we may assume that β_t = α_t, and then we have β_i≤α_i for all i. Since
   ∑_i=1ⁿa_tiα_i = α_t = β_t = ∑_i=1ⁿa_tiβ_i,
   we see that β_i = α_i for all i and the result follows.

7. Set a_n = f (n)². Then squaring f (n + 1) = 2√f (n)²+n, we obtain a_n+1 = 4a_n + 4n. We solve this recurrence relation in a similar way to solving the corresponding first order differential equation y' = 4y + 4t. The solution to a_n+1 = 4a_n is a_n = C4ⁿ for some constant n. Then we look for a solution to a_n+1 = 4a_n + 4n in the form a_n = An + B, where A, B are constants to be determined. Plugging this into the recurrence relation, we obtain A(n + 1) + B = 4An + 4B + 4n, and then equating the coefficients of n and the constant term, we find that A = - 4/3, B = - 4/9. Therefore a_n = C4ⁿ - 4n/3 - 4/9, and then plugging in a₁ = 1, we see that C = 25/36 and we conclude that a_n = 25·4ⁿ/36 - 4n/3 - 4/9. We now need to calculate ∑_n=1^Na_n. This is
   25(4^N -1)/27 - 2N²/3 - 10N/9.

8. We have
   x_n+3 = 19x_n+2/(94_n+1) = 19²/(94²x_n)
   and we deduce that x_n+6 = x_n for all nonnegative integers n. It follows that ∑_n=0^∞x_6n/2ⁿ = ∑_n=0^∞10/2ⁿ = 20.