10th VTRMC, 1988, Solutions

1. Let ABDE be the parallelogram S and let the inscribed circle C have center O. Thus ∠AED = θ. Let S touch C at P, Q, R, T. It is well known that S is a rhombus; to see this, note that EP = ET, AP = AQ, BQ = BR and DR = DT. In particular O is the intersection of AD and EB, ∠EOD = π/2 and ∠OED = θ/2. Let x = area of S. Then x = 4 times area of EOD. Since ED = ET + TD = r cotθ/2 + r tanθ/2, we conclude that x = 2r²(cotθ/2 + tanθ/2).

   
   
   

2. Let the check be for x dollars and y cents, so the original check is for 100x + y cents. Then 100y + x - 5 = 2(100x + y). Therefore 98y - 196x = 5 + 3x. Of course, x and y are integers, and presumably 0≤x, y≤99. Since 98 divides 5 + 3x, we see that x = 31 and hence y = 2x + (5 + 3x)/98 = 63. Thus the original check was for $31.63.

3. If we differentiate y(x) + ∫₁^xy(t) dt = x² with respect to x, we obtain y' + y = 2x. This is a first order linear differential equations, and the general solution is y = Ce^-x + 2x - 2, where C is an arbitrary constant. However when x = 1, y(1) = 1, so 1 = C/e + 2 - 2 and hence C = e. Therefore y = 2x - 2 + e^1-x.

4. If a = 1, then a² + b² = 2 = ab + 1 for all n, and we see that a² + b² is always divisible by ab + 1. From now on, we assume that n≥2.

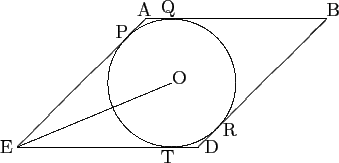
   Suppose aⁿ⁺¹ + 1 divides a² + a²ⁿ, where n is a positive integer. Then aⁿ⁺¹ + 1 divides a^n-1 - a² and hence aⁿ⁺¹ + 1 divides a⁴ + 1. Thus in particular n≤3. If n = 3, then aⁿ⁺¹ +1 = a⁴ + 1 divides a² + a²ⁿ = a² + a⁶. If n = 1, then a² + 1 divides 2a² implies a² + 1 divides 2, which is not possible. Finally if n = 2, we obtain a³ + 1 divides a² + a⁴, so a³ + 1 divides a² - a which again is not possible.

   We conclude that if a > 1, then a² + b² is divisible by ab + 1 if and only if n = 3.

5. Using Rolle's theorem, we see that f is either strictly monotonic increasing or strictly monotonic decreasing; without loss of generality assume that f is monotonic increasing. Then f'(X)≥2 for all x, so |α - x₀| < .00005. Thus the smallest upper bound is .00005.

6. f (x) = ax - bx³ has an extrema when f'(x) = 0, that is a - 3bx² = 0, so x = ±a/(√3b). Then f (x) = ±2a²(3√3b). Since f has 4 extrema on [- 1, 1], two of the extrema must occur at ±1. Thus we have | a - b| = 1. Thus a possible choice is a = .1 and b = 1.1.

7. (a)

   f ([0, 1]) = [0, 1/3]∪[2/3, 1]

   f (f ([0, 1])) = [0, 1/9]∪[2/9, 3/9]∪[6/9, 7/9]∪[8/9, 1]

   f (f (f ([0, 1]))) = [0, 1/27]∪[2/27, 3/27]∪[6/27, 7, 27]∪[8/27, 9/27]∪

   [18/27, 19/27] ∪[20/27, 21/27]∪[24/27, 25/27]∪[26/27, 1]

   
   

   
   
   

   (b)

   Let T⊆R be a bounded set such that f (T) = T. First note that T contains no negative numbers. Indeed if T contains negative numbers, let t₀ = inf_t∈Tt and choose t₁∈T with t₁ < t₀/3. Then there is no t∈T with f (t) = t₁.

   Therefore we may assume that T contains no negative numbers. Now suppose 1/2∈T. Since (x + 2)/3 = 1/2 implies x = - 1/6, we see that 3/2∈T. Now let t₂ = sup_t∈Tt and choose t₃∈T such that t₃ > (t₂ + 2)/3. Since f (T) = T, we see that there exists s∈T such that f (s) > (t₂ + 2)/3, which is not possible.

   We conclude that there is no bounded subset T such that f (T) = T and 1/2∈T.

8. If we have a triangle with integer sides a, b, c, then we obtain a triangle with integer sides a + 1, b + 1, c + 1. Conversely if we have a triangle with integer sides a, b, c and the perimeter a + b + c is even, then none of a, b, c can be 1 (because in a triangle, the sum of the lengths of any two sides is strictly greater than the length of the third side). This means we can obtain a triangle with sides a - 1, b - 1, c - 1. We conclude that T(n) = T(n - 3) if n is even.