32nd VTRMC, 2010, Solutions

1. It is easily checked that 101 is a prime number (divide 101 by the primes whose square is less than 101, i.e. the primes ≤7). Therefore for 1≤r≤100, we may choose a positive integer q such that rq≡1 mod 101. Since (I + A + ... + A¹⁰⁰)(I - A) = I - A¹⁰¹, we see that A¹⁰¹ = I, in particular A is invertible with inverse A¹⁰⁰. Suppose 1 < n≤100 and set r = 101 - n. Then 1≤r≤100 and Aⁿ + ... + A¹⁰⁰ is invertible if and only if I + ... + A^r-1 is invertible. We can think of I + ... + A^r-1 as (I - A^r)/(I - A), which should have inverse (I - A)/(I - A^r). However A = (A^r)^q and so (I - A)/(I - A^r) = I + A^r + ... + (A^r)^q-1. It is easily checked that
   (I + ... + A^r-1)(I + A^r + ... + (A^r)^q-1) = I.
   It follows that Aⁿ + ... + A¹⁰⁰ is invertible for all positive integers n≤100. We conclude that Aⁿ + ... + A¹⁰⁰ has determinant ±1 for all positive integers n < 100.

2. First we will calculate f_n(75)mod 16. Note that if a, b are odd positive integers and a≡b mod 16, then a^a≡b^bmod 16. Also 3³≡11 mod 16 and 11¹¹≡3 mod 16. We now prove by induction on n that f_2n-1(75)≡11 mod 16 for all n∈N. This is clear for n = 1 so suppose f_2n-1(75)≡11 mod 16 and set k = f_2n-1(75) and m = f_2n(75). Then

   f_2n(75)≡k^k≡11¹¹ ≡3 mod 16

   f_2n+1(75)≡m^m≡3³ ≡11 mod 16

   
   
   and the induction step is complete. We now prove that f_n(a)≡f_n+2(a)mod 17 for all a, n∈N with a prime to 17 and n even. In fact we have
   f_n+1(a)≡a³mod 17,    f_n+2(a)≡(a³)¹¹≡a mod 17.
   Thus f₁₀₀(75)≡f₂(75)mod 17. Therefore f₁₀₀(75)≡7¹¹≡14 mod 17.

3. First note the e^2πi/7 satisfies 1 + x + ... + x⁶ = 0, so by taking the real part, we obtain ∑_n=0ⁿ⁼⁶cos 2nπ/7 = 0. Since cos 2π/7 = cos 12π/7, cos 4π/7 = cos 10π/7 = - cos 3π/7 and cos 6π/7 = cos 8π/7 = - cosπ/7, we see that 1 - 2 cosπ/7 + 2 cos 2π/7 - 2 cos 3π/7 = 0.

   Observe that if 1 - 2 cosθ +2 cos 2θ -2 cos 3θ = 0, then by using cos 2θ = 2 cos²θ - 1 and cos 3θ = 4 cos³θ -3 cosθ, we find that cosθ satisfies 8x³ -4x² - 4x + 1 = 0. Thus in particular cosπ/7 satisfies this equation. Next note that 1 - 2 cos 3π/7 + 2 cos 6π/7 - 2 cos 9π/7 = 1 - 2 cos 3π/7 - 2 cosπ/7 + 2 cos 2π/7, so cos 3π/7 is also a root of 8x³ -4x² - 4x + 1. Finally since the sum of the roots of this equation is 1/2, we find that -cos 2θ is also a root. Thus the roots of 8x³ -4x² - 4x + 1 are cosπ/7, -cos 2π/7, cos 3π/7.

4. The equation 4A + 3C = 540^o tells us that A = 3B. Let D on BC such that ∠ADC = 3B, and then let E on BD such that ∠AED = 2B.

   
   
   

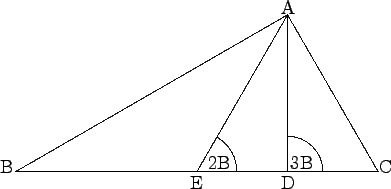
   Since triangles ABD and AED are similar, we see that

   BD/AD = AD/ED = AB/AE.
   Also BE = AE because B = ∠BAE, and BE = BD - BE. We deduce that BD² = AD² + AB·AD. Since BD = BC - CD, we conclude that (BC - CD)² = AD² + AB·AD.

   Next triangles ABC and ADC are similar, consequently

   BC/AC = AB/AD = AC/CD.
   Thus AD = AB·AC/BC and CD = AC²/BC. We deduce that
   (a - b²/a)² = c²b²/a² + c²b/a.
   Therefore (a² - b²)² = bc²(a + b) and the result follows.

5. Let X denote the center of A, let Y denote the center of B, let Z be where A and B touch (so X, Y, Z are collinear), and let θ = ∠PXY. Note that YQ makes an angle 2θ downwards with respect to the horizontal, because ∠QYZ = 3θ.

   
   
   

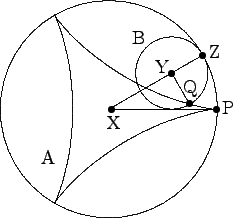
   Choose (x, y)-coordinates such that X is the origin and XP is on the line y = 0. Let (x, y) denote the coordinates of Q. Then we have

   x = 2 cosθ + cos 2θ

   y = 2 sinθ - sin 2θ.

   
   
   By symmetry the area above the x-axis equals the area below the x-axis (we don't really need this observation, but it may make things easier to follow). Also θ goes from 2π to 0 as circle B goes round circle A. Therefore the area enclosed by the locus of Q is

   2∫_π⁰y(dx/dθ) dθ = 2∫_π⁰(2 sinθ - sin 2θ)(- 2 sinθ -2 sin 2θ) dθ = 2∫₀^π(4 sin²θ +2 sinθsin 2θ -2 sin²2θ) dθ = ∫₀^π(4 - 4 cos 2θ +2 cosθ -2 cos 3θ -2 + 2 cos 4θ) dθ = 2π.

   
   

6. Note that if 0 < x, y < 1, then 0 < 1 - y/2 < 1 and 0 < x(1 - y/2) < 1, and it follows that (a_n) is a positive monotone decreasing sequence consisting of numbers strictly less that 1. This sequence must have a limit z where 0≤z≤1. In particular a_n+2 - a_n+1 = a_na_n+1/2 has limit 0, so lim_{n-> ∞}a_na_n+1 = 0. It follows that z = 0.

   Set b_n = 1/a_n. Then b_n+2 = b_n+1/(1 - a_n/2) = b_n+1(1 + a_n/2 + O(a_n²)). Therefore b_n+2 - b_n+1 = b_n+1(a_n/2 + O(a_n²)). Also

   a_n/a_n+1 = (1 - a_n-1/2)^-1 = 1 + O(a_n)
   and we deduce that b_n+2 - b_n+1 = b_n(1 + O(a_n))(a_n/2 + O(a_n²)). Therefore b_n+2 - b_n+1 = 1/2 + O(a_n). Thus given ε > 0, there exists N∈N such that | b_n+1 - b_n -1/2| < ε for all n > N. We deduce that if k is a positive integer, then | b_n+k/k - b_n/k - 1/2| < ε. Thus for k sufficiently large, | b_n+k/(n + k) - 1/2| < 2ε. We conclude that lim_{n-> ∞}b_n/n = 1/2 and hence lim_{n-> ∞}na_n = 2.

7. It will be sufficient to prove that ∑_n=1^∞n²/(1/a₁² + ... +1/a_n²) is convergent. Note we may assume that (a_n) is monotonic decreasing, because rearranging the terms in series ∑a_n does not affect its convergence, whereas the terms of the above series become largest when (a_n) is monotonic decreasing. Next observe that if ∑_n=1^∞a_n = S, then a_n≤S/n for all positive integers n. Now consider (2n)²/(1/a₁² + ... +1/a_2n²). This is ≤(2n)²S/(1/a₁ +2/a₂ + ... +2n/a_2n)≤4n²S/(n²/a_n) = 4Sa_n. The result follows.