28th VTRMC, 2006, Solutions

1. If we write such an integer n in base 3, then it must end in 200...0, because n contains no 1's. But then n² will end in 100...0 and we conclude that there are no positive integers n for which neither n nor n² contain a 1 when written out in base 3.

2. The format of such a sequence must either consist entirely of A's and B's, or must be a block of A's, followed by a single B, followed by a block of C's, followed by a string of A's and B's. In the former case, there are 2ⁿ such sequences. In the latter case, the number of such sequences which have k A's and m C's (where m≥1) is 2^n-m-k-1. Therefore the number of such sequences with k A's is
   ∑_m=1^n-k-12^n-m-k-1 = 2^n-k-1 - 1.
   We deduce that the total number of such sequences is
   ∑_k=0^n-2(2^n-k-1 -1) + 2ⁿ = 2ⁿ -2 - (n - 1) + 2ⁿ = 2ⁿ⁺¹ - (n + 1).
   We conclude that S(10) = 2¹¹ - 11 = 2037.

3. From the recurrence relation F(n) = F(n - 1) + F(n - 2), we obtain

   F(n + 5) = F(n + 4) + F(n + 3) = 2F(n + 3) + F(n + 2) = 3F(n + 2) + 2F(n + 1) = 5F(n + 1) + 3F(n).

   
   
   Thus F(n + 20) = 3⁴F(n) = F(n)mod 5 and we deduce that F(2006) = F(6)mod 20. Since F(6) = 5F(2) + 3F(1) = 8. it follows that F(2006) has remainder 3 after being divided by 5. Also F(n + 5) = 2F(n + 3) + F(n + 2) tells us that F(n + 5) = F(n + 2)mod 2 and hence F(2006) = F(2) = 1 mod 2. We conclude that F(2006) is an odd number which has remainder 3 after being divided by 5, consequently the last digit of F(2006) is 3.

4. Set c_n = (- b_3n-2)ⁿ - (- b_3n-1)ⁿ + (- b_3n)ⁿ. Then the series ∑_n=1^∞c_n can be written as the sum of the three series
   ∑_n=1^∞(- 1)ⁿb_3n-2,    ∑_n=1^∞ - (- 1)ⁿb_3n-1,    ∑_n=1^∞(- 1)ⁿb_3n.
   Since each of these three series is alternating in sign with the absolute value of the terms monotonically decreasing with limit 0, the alternating series test tells us that each of the series is convergent. Therefore the sequence s_k : = ∑_n=1^3k(- 1)ⁿb_n is convergent, with limit S say. Since lim_{n- > ∞}b_n = 0, it follows that ∑_n=1^∞(- 1)ⁿb_n is also convergent with sum S.

5. We will model the solution on the method reduction of order; let us try a solution of the form y = u sin t where u is a function of t. Then y' = u'sin t + u cos t and y'' = u''sin t + 2u'cos t - u sin t. Plugging into y'' + py' + qy = 0, we obtain u''sin t + u'(2 cos t + p sin t) + u(p cos t + q sin t - sin t) = 0. We set
   u''sin t + u'(2 cos t + p sin t) = 0    and    p cos t + q sin t - sin t = 0.
   There are many possibilities. We want u = t² to satisfy u'' + u'(2 cos t + p sin t)/sin t = 0. Since u = t² satisfies u'' - u'/t = 0, we set 2 cot t + p = - 1/t, and then

   p = - 1/t - 2 cot t,

   q = 1 - p cot t = 1 + (cot t)/t + 2 cot²t,

   f = t²sin t.

   
   
   Then p and q are continuous on (0,π) (because 1/t and cot t are continuous on (0,π)), and y = sin t and y = f (t) satisfy u'' + pu' + qu = 0. Also f is infinitely differentiable on the whole real line (- ∞,∞) and f (0) = f'(0) = f''(0) = 0.

6. Let β = ∠QBP and γ = ∠QCP. Then the sine rule for the triangle ABC followed by the double angle formula for sines, and then the addition rules for sines and cosines yields

   (AB + AC)/BC = (sin 2β + sin 2γ)/(sin(2β +2γ)) = (2 sin(β + γ)cos(β - γ))/(2 sin(β + γ)cos(β + γ)) = (cosβcosγ + sinβsinγ)/(cosβcosγ - sinβsinγ) = (1 + tanβtanγ)/(1 - tanβtanγ).

   
   
   Since tanβtanγ = (PQ/BQ)(PQ/QC) = 1/2, we see that (AB + AC)/BC = 3 and the result is proven.

7. We will call the three spheres A, B, D and let their centers be P, Q, R respectively. Then PQR is an equilateral triangle with sides of length 1. So we will let O = (0, 0, 0), P = (0,√3/2, 0), Q = (- 1/2, 0, 0), R = (1/2, 0, 0), and X = (0, 1/(2√3), 0). Then M can be described as the cylinder C with cross-section PQR which is bounded above and below by the spheres A, B, D. Let V denote the space above ORX. We now have the following diagram.

   
   
   

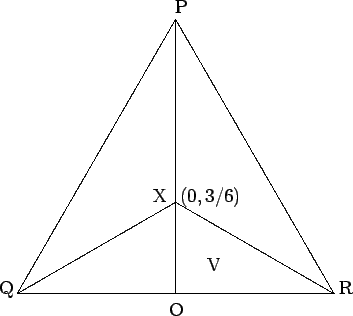
   By symmetry, the mass of M is 12$\iiint_{V}^{}$zdV. Also above QRX, the mass M is bounded above by the A, which has equation z = √1-x²-(y-√3/2)², and the equation of the line XR in the xy-plane is x + √3y = 1/2. Therefore the mass of M is