- The answer is no. One example is
Then
det M =/= 0 (expand by the fourth row), whereas
det N = 0
(fourth row consists entirely of 0's). Therefore M is invertible
and N is not invertible, as required.
- For n a non-negative integer, as n increases from n to n + 6,
we add 3 twice, 1 twice and 2 twice to f (n); in other words
f (n + 6) = f (n) + 12. We deduce that f (n) = 2n when n = 0 (mod 6).
- Let sn denote the number of strings of length n with no three
consecutive A's. Thus s1 = 3, s2 = 9 and s3 = 26.
We claim that we have the following recurrence relation:
sn = 2sn-1 +2sn-2 +2sn-3 (n>3).
The first term on the right hand side indicates the number of such
strings which begin with B or C; the second term indicates the
number of such strings which begin with AB of AC, and the third
term indicates the number of such strings which begin with AAB or
AAC. Using this recurrence relation, we find that s4 = 76, s5 = 222 and s6 = 648. Since the total number of strings is 36,
we conclude that the probability of a string on 6 symbols not
containing 3 successive A's is
648/36 = 8/9.
- The answer is no. Let us color the chess board in the usual way with
alternating black and white squares, say the corners are colored with
black squares. Then by determining the number of black squares in
each row, working from top to bottom, we see that the number of black
squares is
4 + 4 + 5 + 4 + 4 + 4 + 5 + 4 + 4 = 38.
Since there are 78 squares in all, we see that the number of white
squares is 40. Now each domino cover 1 white and 1 black square, so
if the board could be covered by dominoes, then there would be an
equal number of black and white squares, which is not the case.
- Expanding the sine, we have
f (
x) = cos
x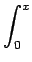
sin(
t2 -
t) d
t + sin
x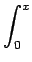
cos(
t2 -
t) d
t.
Therefore
| f'(x) |
= cos x sin(x2 - x) - sin x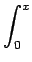 sin(t2 - t) dt sin(t2 - t) dt |
|
| |
+sin x cos(x2 - x) + cos x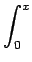 cos(t2 - t) dt, cos(t2 - t) dt, |
|
| f''(x) |
= - sin x sin(x2 - x) + (2x - 1)cos x cos(x2 - x) |
|
| |
-sin x sin(x2 - x) - cos x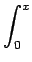 sin(t2 - t) dt sin(t2 - t) dt |
|
| |
+cos x cos(x2 - x) + (1 - 2x)sin x sin(x2 - x) |
|
| |
-sin x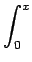 sin(t2 - t) dt + cos x sin(x2 - x). sin(t2 - t) dt + cos x sin(x2 - x). |
|
We deduce that
| f (x) + f''(x) |
= (2x + 1)(cos x cos(x2 - x) - sin x sin(x2 - x)) |
|
| |
= (2x + 1)cos x2. |
|
Set
g(x) = f''(x) + f (x). To find
f(12)(0) + f(10)(0), we need to compute
g(10)(0), which we can find by
considering the coefficient of x10 in the Maclaurin series
expansion for
(2x + 1)cos x2. Since
cos x2 = 1 - x4/2! + x8/4! - x12/6! + ..., we see that this coefficient is 0.
Therefore
g(10)(0) = 0 and the result follows.
- Suppose first that there is an infinite subset S such that each
person only knows a finite number of people in S.
Then pick a person
A1 in S. Then there is an infinite subset S1 of S
containing A1 such that A1 knows nobody in S1. Now choose a
person A2 other than A1 in S1. Then there is an infinite
subset S2 of S1 containing
{A1, A2} such that nobody in
S2 knows A2. Of course nobody in S2 will know A1 either.
Now choose a person A3 in S2 other than A1 and A2. Then
nobody from
{A1, A2, A3} knows each other. Clearly we can
continue this process indefinitely to obtain an arbitrarily large
number of people who don't know each other.
Therefore we may assume in any infinite subset of people there is a
person who knows an infinite number of people. So we can pick a
person B1 who knows infinitely many people T1. Then we can
pick a person B2 in T1 who knows an infinite number of people
T2 of T1, because we are assuming in any infinite subset of
people, there is somebody who knows infinitely many of them. Of
course, B1 and B2 know all the people in T2. Now choose
a person B3 in T2 who knows an infinite number of people in
T2. Then
{B1, B2, B3} know each other. Clearly we can
continue this process indefinitely to obtain an arbitrarily large
number of people who know each other.
Remark A simple application of the axiom of choice shows
that we can find an infinite number of people in the party such that
either they all know each other or they all don't know each other.
- Set
bn = 1 - an+1/an. Let us suppose to the contrary that
S| bn| is convergent. Then
limn-->
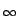 bn = 0, so
may assume that
| bn| < 1/2 for all n. Now
bn = 0, so
may assume that
| bn| < 1/2 for all n. Now
| an+1 |
= a1(1 - b1)(1 - b2)...(1 - bn), |
|
hence
|
| ln(an+1) |
= ln a1 + ln(1 - b1) + ln(1 - b2) + ... + ln(1 - bn). |
|
Since
limn--> 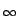 an = 0, we see that
limn-->
an = 0, we see that
limn--> 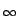 ln(an) = -
ln(an) = - 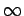 . Now
ln(1 - b)> - 2| b| for | b| < 1/2;
one way to see this is to observe that
1/(1 - x) < 2 for
0 < x < 1/2 and then to integrate between 0
and | b|. Therefore
limn-->
. Now
ln(1 - b)> - 2| b| for | b| < 1/2;
one way to see this is to observe that
1/(1 - x) < 2 for
0 < x < 1/2 and then to integrate between 0
and | b|. Therefore
limn--> 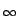 (- 2| b1| - ... -2| bn|) = -
(- 2| b1| - ... -2| bn|) = - 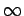 . This proves that
S| bn| is divergent and the
result follows.
. This proves that
S| bn| is divergent and the
result follows.