- The probability of p gains is the coefficient of
(1/2)p(1/2)n - p in
(1/2 + 1/2)n. Therefore, without the insider trading scenario,
on average the investor will have
10000(3/5 + 9/20)n dollars at
the end of n days. With the insider trading, the first term
(3/5)n
becomes 0. Therefore on average the investor will have
10000(21/20)n - 10000(3/5)n
dollars at the end of n days.
- We have
-ln(1 -
x) =
x +
x2/2 +
x3/3 + ... =
Si = 1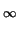
(
xn)/
n.
| (1 - x)ln(1 - x) |
= - x + x2/2 + x3/6 + ... |
|
| |
= - x + Si = 1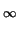 xn + 1(1/n - 1/(n + 1)) = - x + Si = 1 xn + 1(1/n - 1/(n + 1)) = - x + Si = 1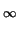 xn + 1/(n(n + 1)). xn + 1/(n(n + 1)). |
|
Dividing by x, we deduce that
Sn = 1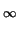 xn
xn/(
n(
n + 1)) = 1 + ((1 -
x)ln(1 -
x))/
x
for
x =/= 0, and the sum is 0 for x = 0.
- Let I denote the 2 by 2 identity matrix.
Since A = A-1, we see that A2 = I and hence
the eigenvalues
l of A must satisfy
l2 = 1, so
l = ±1. First consider the
case
det A = 1. Then A has a repeated eigenvalue
±1, and
A is similar to
where
r = ±1 and s = 0 or 1. Since A2 = I, we see that s = 0 and
we conclude that
A = ±I.
Now suppose
det A = - 1. Then the eigenvalues of A must be
1, - 1, so the trace of A must be 0, which means that A has the
form
where a, b are complex numbers satisfying
a2 + b2 = 1. Therefore
b = (1 - a2)1/2 (where the exponent 1/2 means one of the two
complex numbers whose square is 1 - a2). We conclude that the
matrices satisfying
A = A' = A-1 are
±I and
| | ( |
| | a |
(1 - a2)1/2 |
| |
(1 - a2)1/2 |
- a |
|
) |
where a is any complex number.
- Set
R = e2pi/7 = cos 2p/7 + isin 2p/7.
Since
R =/= 1 and
R7 = 1, we see that
1 + R + ... + R6 = 0. Now
for n an integer,
Rn = cos 2np/7 + isin 2np/7. Thus by
taking the real parts and using
cos(2p - x) = cos x,
cos(p - x) = - cos x, we obtain
1 + 2cos(2p/7) - 2cos(p/7) - 2cos(3p/7) = 0.
Since
cosp/7 + cos 3p/7 = 2cos(2p/7)(cosp/7), the
above becomes
4cos(2p/7)cos(p/7) - 2cos(2p/7) = - 1.
Finally
cos(2p/7) = 2cos2(p/7) - 1, hence
(2cos2(p/7) - 1)(4cos(p/7) - 2) = - 1 and we conclude that
8cos3(p/7) - 4cos2(p/7) - 4cos(p/7) = - 1. Therefore
the rational number required is -1/4.
- Since
/ ABC + / PQC = 90 and
/ ACB + / PRB = 90, we see that
/ QPR = / ABC + / ACB. Now
X, Y, Z being the midpoints of BC, CA, AB respectively tells
us that AY is parallel to ZX, AZ is parallel to XY,
and BX is parallel to YZ. We deduce that
/ ZXY = / BAC and hence
/ QPR + / ZXY = 180.
Therefore the points P, Z, X, Y lie on a circle and we deduce that
/ QPX = / ZYX. Using BZ parallel to XY and BX
parallel to ZY from above, we conclude that
/ ZYX = / ABC. Therefore
/ QPX + / PQX = / ABC + / PQX = 90 and the
result follows.
- Set g = f2. Note that g is continuous,
g3(x) = x for all
x, and f (x) = x for all x if and only if g(x) = x for all
x. Suppose
y e [0, 1] and
f (y) =/= y. Then the numbers
y, f (y), f2(y) are distinct. Replacing y with f (y) or f2(y)
and f with g if necessary, we may assume that
y < f (y) < f2(y). Choose
a e (f (y), f2(y)).
Since f is continuous, there exists
p e (y, f (y)) and
q e (f (y), f2(y)) such that
f (p) = a = f (q).
Thus
f (p) = f (q), hence
f3(p) = f3(q) and we deduce that
p = q. This is a contradiction because
p < f (y) < q, and the
result follows.
- Let the tetrahedron have vertices A, B, C, D and let X denote the
midpoint of BC. Then
AX =
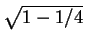 =
= 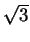 /2 and we see that ABC has area
/2 and we see that ABC has area
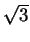 /4. Let
R, S, T, U denote the regions vertically above and distance at
most 1 from
ABC, BCD, ABD, ACD respectively. Then the volumes of
R, S, T and U are all
/4. Let
R, S, T, U denote the regions vertically above and distance at
most 1 from
ABC, BCD, ABD, ACD respectively. Then the volumes of
R, S, T and U are all
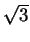 /4. Since these regions are
disjoint, they will contribute
/4. Since these regions are
disjoint, they will contribute 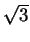 to the volume required.
to the volume required.
Let Y denote the point on AX which is vertically below D. Then
Y is the center of ABC (i.e. where the medians meet), in
particular
/ YBX = p/6 and we see that
BY = 1/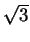 .
Therefore
DY =
.
Therefore
DY = 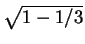 =
= 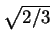 and we deduce that
ABCD has volume
and we deduce that
ABCD has volume
Next consider the region which is distance
1 from BC and is between
R and S. We need the angle between R and S, and for this we
find the angle between DX and DY. Now
DX = AX = 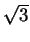 /2 and
DY =
/2 and
DY = 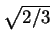 . Therefore
XY =
. Therefore
XY = 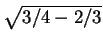 = 1/(2
= 1/(2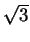 ).
If
q = / YDX, then
sinq = XY/DX = 1/3. We
deduce that the angle between R and S is
p/2 + q = p/2 + sin-11/3. Therefore the region at distance 1 from BC and
between R and S has volume
p/4 + (sin-11/3)/2. There are
6 such regions, which contribute
3p/2 + 3sin-11/3 to the
volume required.
).
If
q = / YDX, then
sinq = XY/DX = 1/3. We
deduce that the angle between R and S is
p/2 + q = p/2 + sin-11/3. Therefore the region at distance 1 from BC and
between R and S has volume
p/4 + (sin-11/3)/2. There are
6 such regions, which contribute
3p/2 + 3sin-11/3 to the
volume required.
For the remaining volume, we shrink the sides of the tetrahedron to
zero. This keeps the remaining volume constant, but the volumes
above go to zero. We are left with the volume which is distance 1
from the center of the pyramid, which is
4p/3. Since
3p/2 + 4p/3 = 17p/6, we conclude that the volume
of the region consisting of points which are distance at most 1 from
ABCD is
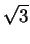 +
+ 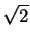 /12 + 17p/6 + 3sin-1(1/3)
/12 + 17p/6 + 3sin-1(1/3) 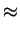 11.77.
Other expressions for this are
11.77.
Other expressions for this are
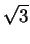 +
+ 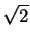 /12 + 13p/3 - 3cos-1(1/3)
and
/12 + 13p/3 - 3cos-1(1/3)
and
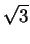 +
+ 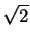 /12 + 13p/3 - 6sin-1(1/
/12 + 13p/3 - 6sin-1(1/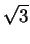 ).
).
![]() .
Therefore
DY =
.
Therefore
DY = ![]() =
= ![]() and we deduce that
ABCD has volume
and we deduce that
ABCD has volume
![]() /2 and
DY =
/2 and
DY = ![]() . Therefore
XY =
. Therefore
XY = ![]() = 1/(2
= 1/(2![]() ).
If
q = / YDX, then
sinq = XY/DX = 1/3. We
deduce that the angle between R and S is
p/2 + q = p/2 + sin-11/3. Therefore the region at distance 1 from BC and
between R and S has volume
p/4 + (sin-11/3)/2. There are
6 such regions, which contribute
3p/2 + 3sin-11/3 to the
volume required.
).
If
q = / YDX, then
sinq = XY/DX = 1/3. We
deduce that the angle between R and S is
p/2 + q = p/2 + sin-11/3. Therefore the region at distance 1 from BC and
between R and S has volume
p/4 + (sin-11/3)/2. There are
6 such regions, which contribute
3p/2 + 3sin-11/3 to the
volume required.
![]() +
+ ![]() /12 + 17p/6 + 3sin-1(1/3)
/12 + 17p/6 + 3sin-1(1/3) ![]() 11.77.
Other expressions for this are
11.77.
Other expressions for this are
![]() +
+ ![]() /12 + 13p/3 - 3cos-1(1/3)
and
/12 + 13p/3 - 3cos-1(1/3)
and
![]() +
+ ![]() /12 + 13p/3 - 6sin-1(1/
/12 + 13p/3 - 6sin-1(1/![]() ).
).