- We calculate the volume of the region which is in the first octant
and above
{(x, y, 0) | x>y}; this is 1/16 of the required
volume. The volume is above R, where R is the region in the
xy-plane and bounded by y = 0, y = x and
y =
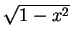 ,
and below
z =
,
and below
z = 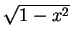 . This volume is
. This volume is
| |
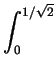 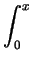 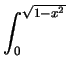 dzdydx + dzdydx + 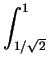 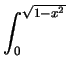 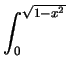 dzdydx dzdydx |
|
| |
= 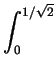 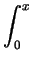 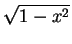 dydx + dydx + 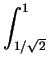 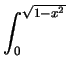 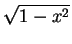 dydx dydx |
|
| |
= 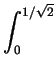 x x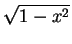 dx + dx + 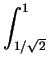 (1 - x2) dx (1 - x2) dx |
|
| |
= [- (1 - x2)3/2/3]01/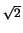 + [x - x3/3]1/ + [x - x3/3]1/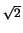 1 1 |
|
| |
= 1/3 - 1/(6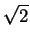 ) + 2/3 + 1/(6 ) + 2/3 + 1/(6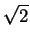 ) - 1/ ) - 1/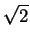 |
|
| |
= 1 - 1/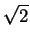 . . |
|
Therefore the required volume is
16 - 8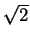 .
.
![\includegraphics [scale=.89]{cylinders.eps}](img10.gif)
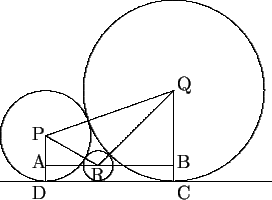
- Let the circle with radius 1 have center P, the circle with radius 2
have center Q, and let R be the center of the third circle, as
shown below. Let
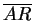 = a,
= a,
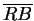 = b, and let
the radius of the third circle be r. By
Pythagoras on the triangles PAR and QRB, we obtain
= b, and let
the radius of the third circle be r. By
Pythagoras on the triangles PAR and QRB, we obtain
(1 - r)2 + a2 = (1 + r)2, (2 - r)2 + b2 = (2 + r)2.
Therefore a2 = 4r and b2 = 8r. Also
(a + b)2 + 1 = 9, so
2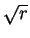 + 2
+ 2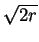 =
= 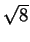 and we deduce that
r = 6 - 4
and we deduce that
r = 6 - 4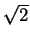 .
.
- Let m, n be a positive integers where
m < n. For each
m X m square in an
n X n grid, replace it with the
(m - 1) X (m - 1) square obtained by deleting the first row and column; this
means that the
1 X 1 squares become nothing. Then these new
squares (don't include the squares which are nothing)
are in a one-to-one correspondence with the squares of the
(n - 1) X (n - 1) grid obtained by deleting the first row and
column of the
n X n square. Therefore Sn - 1 is the number
of squares in an
n X n grid which have size at least
2 X 2. Since there are n2
1 X 1 squares in an
n X n
grid, we deduce that
Sn = Sn - 1 + n2.
Thus
S8 = 12 + 22 + ... + 82 = 204.
- If
p < q < (p + 1)2, then p divides q if and only if q = p2, p2 + p or p2 + 2p. Therefore if ak = p2, then
ak + 3 = (p + 1)2. Since a1 = 12, we see that
a10000 = (1 + 9999/3)2 = 33342 = 11115556.
- Let
an = nnxn/n!. First we use the ratio test:
an + 1/an = ((n + 1)n + 1xn + 1n!)/(nnxn(n + 1)!) = (1 + 1/n)nx.
Since
limn - > 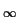 (1 + 1/n)n = e, we see that the interval of
convergence is of the form
{ - 1/e, 1/e}, where we need to decide
whether the interval is open or closed at its two endpoints. By
considering
(1 + 1/n)n = e, we see that the interval of
convergence is of the form
{ - 1/e, 1/e}, where we need to decide
whether the interval is open or closed at its two endpoints. By
considering
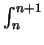 dx/x, we see that
dx/x, we see that
1/(n + 1) < ln(1 + 1/n) < (1/n + 1/(n + 10))/2 < 3/(3n + 1)
because 1/n is a concave function,
consequently
(1 + 1/n)n + 1/3 < e < (1 + 1/n)n + 1. Therefore when
| x| = 1/e, we see that | an| is a decreasing sequence.
Furthermore by induction on n and
the left hand side of the last
inequality, we see that
| an| < 1/![$ \sqrt[3]{n}$](img19.gif) . Thus when x = - 1/e,
we see that
limn - >
. Thus when x = - 1/e,
we see that
limn - > 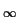 an = 0 and it follows that the
given series is convergent, by the
alternating series test. On the other hand when x = 1/e, the series
is
Snn/(enn!). By induction on n and the above
inequality,
we see that
nn/(en/n!) > 1/(en) for all n > 1.
Since
S1/n is divergent,
we deduce that the given series is divergent when x = 1/e,
consequently the interval of convergence is
[- 1/e, 1/e).
an = 0 and it follows that the
given series is convergent, by the
alternating series test. On the other hand when x = 1/e, the series
is
Snn/(enn!). By induction on n and the above
inequality,
we see that
nn/(en/n!) > 1/(en) for all n > 1.
Since
S1/n is divergent,
we deduce that the given series is divergent when x = 1/e,
consequently the interval of convergence is
[- 1/e, 1/e).
- Let
If we can find a
matrix
such that B2 = A or even 4A and
set
f (x) = (ax + b)/(cx + d ), then
f (f (x)) = (3x + 1)/(x + 3). So we want to find a square root of A. The
eigenvalues of A are 2 and 4, and the corresponding eigenvectors
are (1,-1) and (1,1) respectively. Thus if
then
Set
| | C = |
( |
| | 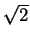 |
0 |
| | 0 |
2 |
|
). |
Then
C2 = XAX-1,
so if we let
B = (X-1CX)2, then B2 = A. Since
we may define (multiply top and bottom by
1 + 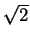 /2)
/2)
f (
x) = ((3 + 2
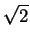
)
x + 1)/(
x + 3 + 2
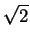
).
Finally we should remark that f still maps
R+ to
R+.
Of course there are many other solutions and answers.
- Choose x
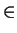 A and y
A and y 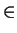 B so that f (xy) is as large as
possible. Suppose we can write xy in another way as ab with a
B so that f (xy) is as large as
possible. Suppose we can write xy in another way as ab with a 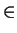 A and b
A and b 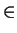 B (so
a =/= x).
Set
g = ax-1 and note that
I =/= g
B (so
a =/= x).
Set
g = ax-1 and note that
I =/= g 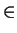 G.
Therefore either
f (gxy) > f (xy) or
f (g-1xy) > f (xy). We
deduce that either
f (ay) > f (xy) or
f (xb) > f (xy), a
contradiction and the result follows.
G.
Therefore either
f (gxy) > f (xy) or
f (g-1xy) > f (xy). We
deduce that either
f (ay) > f (xy) or
f (xb) > f (xy), a
contradiction and the result follows.
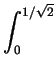
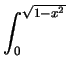 dzdydx +
dzdydx + 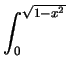
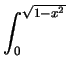 dzdydx
dzdydx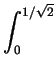
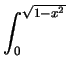
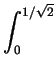 x
x![\includegraphics [scale=.89]{cylinders.eps}](img10.gif)

![]() . Thus when x = - 1/e,
we see that
limn - >
. Thus when x = - 1/e,
we see that
limn - > ![]() an = 0 and it follows that the
given series is convergent, by the
alternating series test. On the other hand when x = 1/e, the series
is
Snn/(enn!). By induction on n and the above
inequality,
we see that
nn/(en/n!) > 1/(en) for all n > 1.
Since
S1/n is divergent,
we deduce that the given series is divergent when x = 1/e,
consequently the interval of convergence is
[- 1/e, 1/e).
an = 0 and it follows that the
given series is convergent, by the
alternating series test. On the other hand when x = 1/e, the series
is
Snn/(enn!). By induction on n and the above
inequality,
we see that
nn/(en/n!) > 1/(en) for all n > 1.
Since
S1/n is divergent,
we deduce that the given series is divergent when x = 1/e,
consequently the interval of convergence is
[- 1/e, 1/e).
![]() /2)
/2)