We describe and illustrate here three programs, pairsnap.c, partsnap.c, and bitwist.c, which are written to run on unix platforms and whose source codes are available from this web site. These programs were written by J. W. Cannon, W. J. Floyd, and W. R. Parry. At the end of the file we describe the program cellsnap.c, which generalizes the frist two of them. We first explain the purposes of the programs.

Let P be a regular cell complex such that P is homeomorphic to a 3-ball and P has a single 3-cell. So each 2-cell is an n-gon with n at least two. Suppose that P has an even number of 2-cells. An edge pairing efor P is a pairing of the faces of P by orientation reversing cellular homeomorphisms. That is for each face f there is a face f' and an orientation reversing cellular homeomorphism e_f from f to f'. We require that (f')' = f and that e_f' = (e_f)^-1.

It is well known that the quotient space obtained from P by identifying each face f with e_f(f) will not generally be a 3-manifold since the link of a vertex may not be a 2-sphere. In fact, the quotient is a 3-manifold exactly if its Euler characteristic is 0. However, one can modify P and the face pairing so that the quotient is a 3-manifold.

Let ~ be the equivalence relation on {edges of P} generated by the relation that d ~ e_f(d) if d is an edge of the face f. The equivalence classes of the edges are called edge cycles. For each edge cycle [d], choose a positive integer m([d]). (m([d]) is called the multiplier of [d].) Now let Q be the cell complex obtained from P by subdividing each edge d of P into #([d])m([d]) subedges. Given a face g of Q, let f be the face of P with |f|=|g|, and let t_g be the orientation preserving cellular homeomorphism of g which takes each vertex v to the adjacent vertex w in the counterclockwise order. Define an edge pairing on Q by e_g = e_f t_g.

Theorem (Cannon, Floyd, and Parry): The quotient of Q under the face pairings is a 3-manifold.

The program pairsnap.c takes as input a data file which gives the combinatorics of the cell complex of P on the 2-sphere and an edge pairing. The program asks the user for the multipliers, and then writes a file for the quotient 3-manifold for input in SnapPea 2.5.

As before, for each edge class [d] let m([d]) ba a positive integer. Now let Q be the cell complex obtained from P by subdividing each edge d of P into n([d])m([d]) subedges. Given a face g of Q, let f be the face of P with |f|=|g|, and let t_g be the orientation preserving cellular homeomorphism of g which takes each vertex v to the adjacent vertex w in the counterclockwise order. Define an edge pairing on Q by e_g = e_f t_g. The quotient of Q under the face pairing is not a manifold, but it is a cell complex whose only vertex has link a torus. The complement of this vertex is a cusped 3-manifold with a single cusp.

The program partsnap.c takes as input a data file which gives the combinatorics of the cell complex of P on the 2-sphere and an edge pairing. The program asks the user for the face f and for the multipliers, and then writes a file for the cusped 3-manifold (obtained by deleting the vertex from the quotient) for input in SnapPea 2.5.

• teta --- For this example, we take P to be a tetrahedron, and choose the face pairing so that each e_f fixes the edge joining f and f'. The following figure shows labels of the faces and edges of a tetrahedron. The associated input file for pairsnap.c, teta.twp, is given below the figure.

  

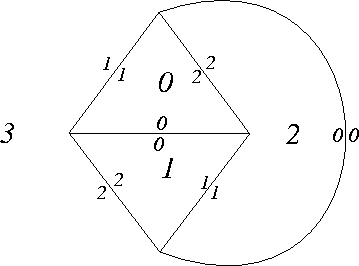
  Number_of_tiles
  4
  Size_of_each_of_these_tiles:
  3 3 3 3
  Tile-ids_--_Adjacent_tiles_in_correct_order:
  0 1 3 2
  1 0 2 3
  2 3 1 0
  3 2 0 1
  Tile-id_--_image_tile-id_and_edge_no_of_image_of_edge-0:
  0 1 0
  1 0 0
  2 3 0
  3 2 0
  

  There are two edge cycles with 1 element and one edge cycle with 4 elements. If you use choose multiplier m for one of the edge cycles with one element and multipliers 1 for other two edge cycles, then the resulting closed manifold is obtained by (m,1) Dehn surgery on the figure-eight knot complement. These are hyperbolic if m is at least 5.

  If you choose multipliers m and n for the edge cycles with 1 element and multiplier p for the edge cycle with 4 elements, then the resulting closed manifold is obtained from the Borromean rings complement with surgery coefficients -m, -n, and 1/p.

  If you instead use partsnap.c and choose 1 for each multiplier (by symmetry, it doesn't matter which face you choose), then the resulting cusped 3-manifold is the figure-eight knot complement.

• hex --- The next figure shows the edge and face labels for a glueing of the hexahedron. The associated input file for pairsnap.c, hex.twp, is shown below the figure.

  

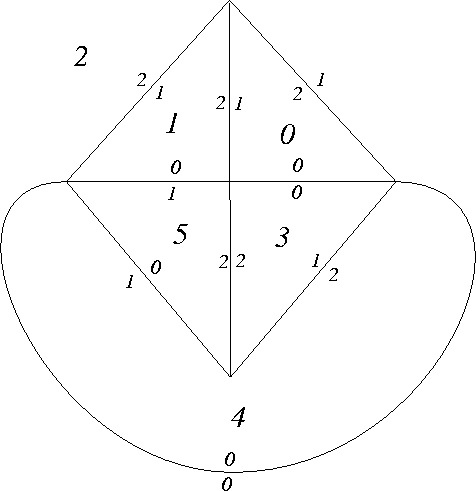
  Number_of_tiles
  6
  Size_of_each_of_these_tiles:
  3 3 3 3 3 3
  Tile-ids_--_Adjacent_tiles_in_correct_order:
  0 3 1 2
  1 5 2 0
  2 4 0 1
  3 0 4 5
  4 2 5 3
  5 4 1 3
  Tile-id_--_image_tile-id_and_edge_no_of_image_of_edge-0:
  0 3 0
  1 5 1
  2 4 0
  3 0 0
  4 2 0
  5 1 1
  

  There are three edge cycles with one element and three edge cycles of with two elements. If you choose each multiplier to be 2, then the resulting closed 3-manifold is hyperbolic with volume approximately 5.1379 and symmetry group of order 48. Hex2.txt gives the SnapPea input file for this example which is produced from pairsnap.c using 2 for each multiplier. Note that SnapPea will not always immediately recognize that this is an input file for a hyperbolic 3-manifold. SnapPea analyzes the manifold by first drilling out a solid torus, and depending on which solid torus it picks it may or may not be able to tell that the 3-manifold is hyperbolic.

• cubea --- In this example, P is a cube and the face pairing identifies opposite faces by translation. There are three edge cycles, each with 4 elements. It follows from the general theory that for any choice of multipliers the resulting closed 3-manifold M has Gromov hyperbolic fundamental group. When each multiplier is 1, the volume of M is approximated 17.663.
• cubeb --- In this example, P is a cube and the face pairing is the antipodal map. Each of the six edge cycles has length two. It follows from the general theory that for any choice of multipliers the closed manifiold M has Gromov hyperbolic fundamental group.i When each multiplier is 1, the resulting closed manifold M is hyperbolc with volume approximately 5.3335 and shortest geodesic of length approximately 1.2659.

lunes --- In this example P has four digons and the face pairing map is the antipodal map. Each of the two edge cyles has two elements.