Mark Embree, Ronald B. Morgan, and Huy V. Nguyen
To appear in SIAM J. Scientific Comp.
Preprint: arXiv:1607.00255 [math.NA] (revised March 2017)
What it does
In 1998 Essai proposed a variant of the GMRES algorithm in which the inner product is changed at each restart, as determined by the current residual vector. From some systems this modification gives much faster convergence; for others, little improvement or even slower convergence. While the promise of this method has attracted attention over the years, our inability to predict the matrices on which excels has limited its adoption. This manuscript proposes that this W-GMRES algorithm performs well when the eigenvectors of the coefficient matrix are localized, i.e., small aside from a few entries. For matrices lacking this property, we propose the W-GMRES-DCT matrix, which incorporates a fast discrete cosine transform into the inner product: this method seems to perform well when the eigenvectors are localized in the Fourier basis (as is often the case for discretizations of constant-coefficient differential equations). The manuscript also shows how to incorporate an inner product in the GMRES-DR algorithm.
Why it matters
W-GMRES seems to have the most impact for difficult problems with small restart parameters.
By better understanding the cases where it succeeds, we can deploy it more strategically.
The W-GMRES-DCT algorithm shows how to extend the benefits of weighted inner products
to a another important class of matrices, and suggests the development of
fast transformations that localize eigenvectors for other specific applications.
Weighting can be combined with deflated restarting to give W-GMRES-DR.
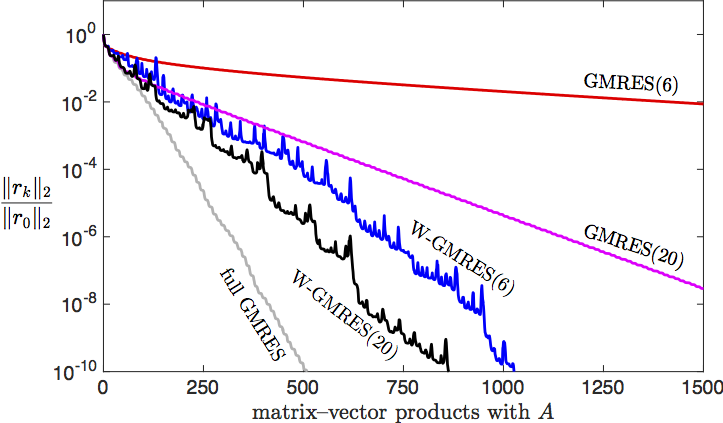
W-GMRES for the Add20 matrix (Essai's example)
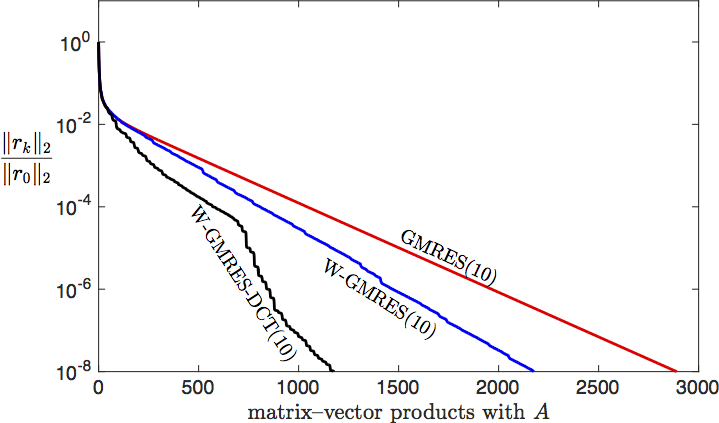
W-GMRES-DCT for a 2d convection diffusion matrix