about
teaching
students
research
return
"Pseudospectra of matrix pencils for transient analysis of differential-algebraic equations"
Mark Embree and Blake Keeler
SIAM J. Matrix Anal. Appl. 38 (2017) 1028-1054. (Copyright SIAM, 2017)
Preprint: arXiv:1601.00044 [math.NA] (revised June 2017)

What it does

Many mathematical models lead to dynamical systems of the form ${\bf E} \dot{\bf x}(t) = {\bf A}{\bf x}(t)$. For example, linear stability analysis involves linearizing a nonlinear system about a fixed point, resulting in a system of this form. To assess stability of that fixed point, one computes eigenvalues of the matrix pencil $({\bf A}, {\bf E})$, i.e., complex $\lambda$ and nonzero ${\bf v}$ such that ${\bf A}{\bf v} = \lambda {\bf E} {\bf v}$. The system is stable if all such eigenvalues $\lambda$ are in the left half of the complex plane. When small perturbations to ${\bf A}$ and/or ${\bf E}$ give eigenvalues in the right-half plane, the original system has a small distance to instability, and its solutions can exhibit transient growth before the eventual asymptotic decay inevitable for a stable system.

How close is a system to instability, and how much transient growth can such as system exhibit? This is a question of eigenvalue perturbation theory, and the pseudospectrum is one tool with which to approach such questions. Previous definitions of the pseudospectrum of a matrix pencil $({\bf A},{\bf E})$ either (1) vary when the system ${\bf E} \dot{\bf x}(t) = {\bf A}{\bf x}(t)$ is premultiplied by a constant matrix, ${\bf T E} \dot{\bf x}(t) = {\bf T A}{\bf x}(t)$, or (2) fail in the important case of differential-algebraic equations (DAEs), where ${\bf E}$ is singular.

This manuscript introduces a new definition of the $\varepsilon$-pseudospectrum $\sigma_\varepsilon({\bf A},{\bf E})$ of a matrix pencil that is designed for analysis of the distance to instability and transient analysis of differential-algebraic equations. We derive the definition, provide theorems that guarantee transient growth when the pseudospectra extend far into the right half-plane, explain how to approximate the definition (in a physically-relevant norm) as a consequence of a large-scale linear stability eigenvalue calculation, and show some examples from fluid dynamics (flow over a backward-facing step and flow over an obstacle), using the IFISS package.

Why it matters

Differential-algebraic equations (and associated descriptor systems in control theory) arise in many important applications. In particular, many fluid mechanics examples give rise to such systems that exhibit transient growth that depends on flow parameters, such as the Reynolds number. This work presents a direct way to apply pseudospectral theory to such problems to obtain a more robust stability analysis than available from studying eigenvalues alone.


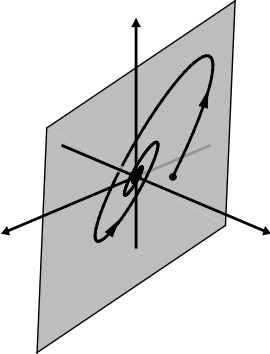
Transient growth of a solution ${\bf x}(t)$ to a DAE ${\bf E} \dot{\bf x}(t) = {\bf A}{\bf x}(t)$ in three dimensions, restricted by the algebraic constraint to a two-dimensional subspace.


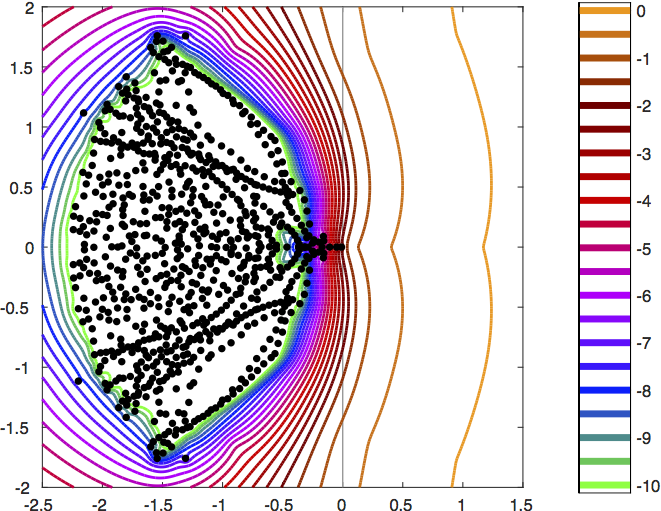
Approximate energy-norm pseudospectra for flow over a backward-facing step, computed with EigTool.


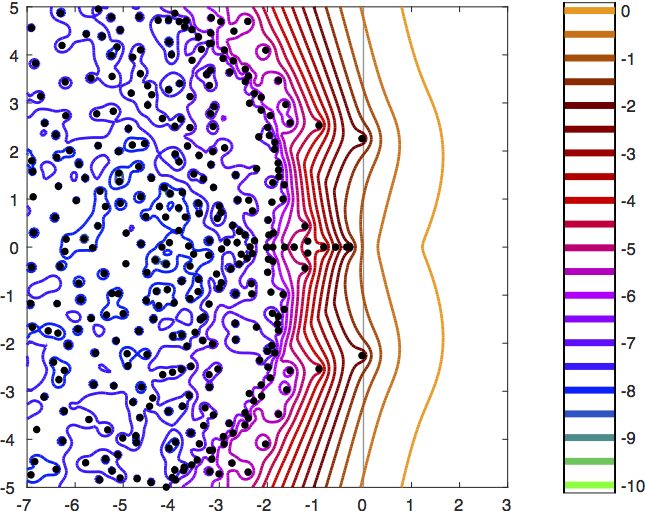
Approximate energy-norm pseudospectra for flow over an obstacle, computed with EigTool.

Resources

${\bf A}$ and $ {\bf E}$ matrices for several examples are available for download (in MATLAB's .mat format). These matrices were all constructed using IFISS package. We thank Howard Elman for his advice about the use of IFISS for linear stability analysis of the backward facing step and obstacle flow problems.

about
teaching
students
research
return