The 1991-2014 Calculus Sequence

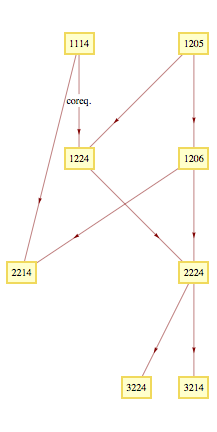
From 1991 until 2014 the freshman-sophomore calculus consisted of 6 courses: 1205-1206 (single variable calculus) , 1114 (elementary linear algebra) , 1224 (vector geometry), 2224 (multivariable calculus), and 2214 (differential equations). The chart at right indicates their prerequisite structure.  (3214, 3224 have been included in the chart as well since they were the 3000-level courses most closely dependent on the content of the calculus-related courses.)  Here are brief descriptions of their contents administration as of 2011. 

1114: Elementary Linear Algebra (2)

• Vector and matrix algebra, linear systems, complex numbers, eigenvalues, determinants, (no linear independence)
• "how-to" emphasis
• All on-line, including course materials, quizzes and tests (all multiple choice)
• Weekly quizzes (unproctored, taken anywhere), up to 4 practice quizzes each week
• Four tests + final (proctored, Emporium).

1224: Vector Geometry (2)

• vector algebra, complex numbers, lines & planes, polar coordinates, parametric curves
• "how-to" emphasis
• text: Greenberg's lecture notes
• one large lecture/week + recitations
• on-line quizzes and tests (all multiple-choice)
• 10 quizzes (unproctored, taken anywhere)
• 3 tests + final (proctored, Emporium)

1205: Calculus (3)

• 38-6 individual sections (F-S)
• limits, continuity, derivatives, and applications (single variable)
• text: Hass-Weir-Thomas
• weekly on-line quizzes (unproctored, taken anywhere), unlimited practice quizzes
  
• 3 exams + final (written, all common time)
  
• At least 15% graded work beyond tests (e.g. homework or in-class quizzes, at discretion of instructor)

1206: Calculus (3)

• 13-20 individual sections (F-S)
• integration, techniques and application, improper integrals, L'Hopital's Rule
• Homework collection at discretion of individual instructor
• text: Hass-Weir-Thomas
  
• Homework collection at discretion of individual instructor
• most sections are 1206C: all testing on-line
• 6 tests, 1^st is "Basic Skills", (proctored, Emporium), unlimited practice tests
  
• commont time final

2214: Introduction to Differential Equations (3)

• 13-16 individual sections (F-S)
• text: Kohler-Johnson
  
• ODEs, undetermined coefficients, x'=Ax, applications
• on-line quizzes at discretion of individual instructor (including choice of procotoring/not)
  
• in-class tests
• on-line final, (proctored, Emporium), the exam is essentially common, but not the time

2224: Multivariable Calculus (3)

• 20-18 individual sections (F-S)
• traditional format, common time final
• text: Hass-Weir-Thomas
  
• f(x₁,x₂, ...), surfaces, level curves, derivatives and multiple integrals, sequences and series

Summary of Concerns and Comments

The following is a brief summary of faculty comments regarding the above courses which were voiced in the Fall 2011 discussions leading to their replacement.

Skills that students are deficient on:

Topic or course-specific comments:

• 1114:
• important topics are missing
• the on-line materials are poor
• 1224:
• Many students take 1114 and 1224 simultaneously.  Would need reorganization to eliminate duplication of vector material. 
• Remove complex numbers, replace with first exposure to cylindrical and spherical coordinates.
• Assign to more than one faculty.
• Course is too watered-down. 
• Course has no purpose except to cover "miscellaneous topics".
• Perhaps infinite series belong here 1224 (not in 2224).
• 1206:
• We should have just one format for 1206 (for fairness).
• 2214:
• Taylor series should be covered in an earlier course, and series solutions of ODEs should be included here.
• Should include more Matlab
• Allowing quiz variations is inefficient.  There should be a unfiorm quiz roughly every 2 weeks.  Each instructor take or leave it.
• Why is 2214 final multiple-choice on-line rather than the same CTE format as the other courses?
• 2224:
• Sequences and series belong somewhere else.
• Put infinite series at the beginning, so they are not neglected.
• Use a common text for 1224, 1205, 1206, 2224 (to facilitate student review).
• Homework and quiz policies should be more uniform across courses.
• Add more recitation sections.
• Where does a discussion of complex numbers belong?
  

General issues and comments:

• Do we want to move to a more computer-based first year calculus?
• The inadequacy of 1114 is the most cited problem. Several suggest replacing 1114 with a full-fledged 3-hour course, and a more conceptual emphasis, including linear independence and bases (not a how-to course for 3x3 matrices).
• Reliance on multiple-choice quizes with little or no graded homework is not effective.  Homework and quiz policies should be more uniform across the courses.
• Get rid of common time finals.
• Practice and repetition are needed to develop operational skills.
• Topics should be revisted multiple times with increasing detail and sophistication.
• What can we learn from the Computational Calculus experiment this year?
• Students do not acquire a conceptual understanding of calculus (even though they may be able to do certain calculations).
• Biggest issue is in the transition to rigorous expectations of 3000-level courses.  A 3-hour sophomore linear algebra course may be the best approach to preparing them for this.
• Students need more exposure to rigorous thinking and arguments.  This should be part of course goals, escalating progressively through the courses.
• How much can we hope to accomplish by adjusting our program structure?
• GTAs are not getting enough experience preparing their own tests.
• We need to be guided by clear goals and principles:
• recognition of appropriate techniques, and ability to implement
• identification of the most important basic skills (given the availability of computers)
• development of mathematical sophistication and conceptual framework
• develop logical reasoning and writing skills, as appropriate
• appreciation of mathematics as an evolving discipline
• development of perspective, ability to formulate questions, "choosing to learn"
• recognizing the appropriate role of computer-based quizes and testing
• developing ability to recognize when the computer can be an effective tool, and ability to use it