As noted in my Research Page, one of my main areas of interest is reduced-order modeling.
Reduced-order modeling refers to building low-dimensional models for large- and infinite-dimensional dynamical systems. "Low" can typically be on the order of 10-100, and "large" can be as large as 10^6 or more. The premise is that there must exist underlying low-dimensional dynamics for the problem and hopefully something like an inertial manifold.
The computer reduced-order models have wide-ranging applications from
- prediction: reduced-order models have their roots in weather forecasting. In fact, the well-known Lorenz equations were developed as a reduced-order model for Benard convection. Today, reduced-order models play a role in determining initial conditions for forecasting and climate models using a procedure known as 4DVar (look here for more details and links).
- control: where the reduced-order model is used to generate feedback control laws or state estimators for complex systems. Recently, reduced-order models have been studied for their potential in solving the Hamilton-Jacobi equations arising in nonlinear feedback control (look here for more details and links).
- optimization: where the reduced-order model is used as a surrogate model in the optimization in problems such as PDE-constrained optimization. (Initial work in this area is being conducted by Ekkehard Sachs.
For nonlinear problems, the current strategy of choice is projection. Thus, reduced-order models are built in two parts. The first is to construct a suitable basis on which to represent the solution. The second is to project the differential equations governing the dynamics onto this basis. For the latter part, Galerkin projection is typically used. Most of the "art" in this field is in building suitable bases and developing fast, reliable algorithms to do this.
Our research group aims to study the entire reduced-order modeling problem (explore improvements in both pieces of the problem).
Here are movies of flow snapshots (solutions courtesy Alexander Hay and Dominique Pelletier, Ecole Polytechnique de Montreal). Note that a mesh containing over 7152 elements, 21626 nodes and over 50000 variables were used to generate this solution. Note the von Karman vortex street at this modest Reynolds number of 100.
The basic idea is to generate low-dimensional global basis functions for this solution. In this example, we use the singular value decomposition; also known as proper orthogonal decomposition (POD), principle component analysis (PCA), Karhunen-Loeve expansion (KLE), empirical orthogonal functions (EOFs), to generate a 12 degree of freedom model (6 basis functions for each component of velocity).
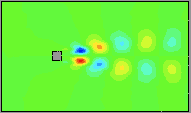
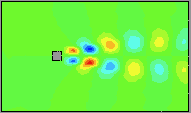
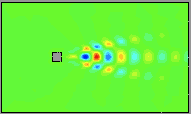
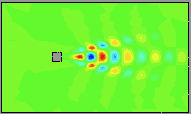

Using this basis, we evolve a 12th order nonlinear differential equation to obtain the following simulations. The movie of the horizontal velocity component follows.
Same time window (one period of oscillation) U_POD.mov
Extrapolation over several periods U_PODextrap.mov or U_PODextrap.avi.
Our research has primarily been to extend the applicability of the traditional POD/Galerkin approach to new settings. These include
- Complex high-Reynolds number flows by developing new ROM closure models
- Improving the accuracy of ROMs in parameter dependent flow problems by developing POD sensitivity basis functions
- Guaranteeing accuracy of reduced-order models using principal interval decomposition
- Developing new methodologies for using ROMs to solve linear feedback control problems for PDEs
- Computing dynamically optimal basis functions
This research was performed from 2005-present and was primarily joint work with:
- Traian Iliescu at Virginia Tech's Interdisciplinary Center for Applied Mathematics, and
- postdocs Imran Akhtar and Alexander Hay,
- students Miroslav Stoyanov and Zhu Wang, and
- Dominique Pelletier at Ecole Polytechnique de Montreal.
Funding was provided by the Air Force Office of Scientific Research under grants FA9550-05-1-0449 and FA9550-08-1-0136 and the National Science Foundation under grants DMS 0513542 and DMS 1016450.





